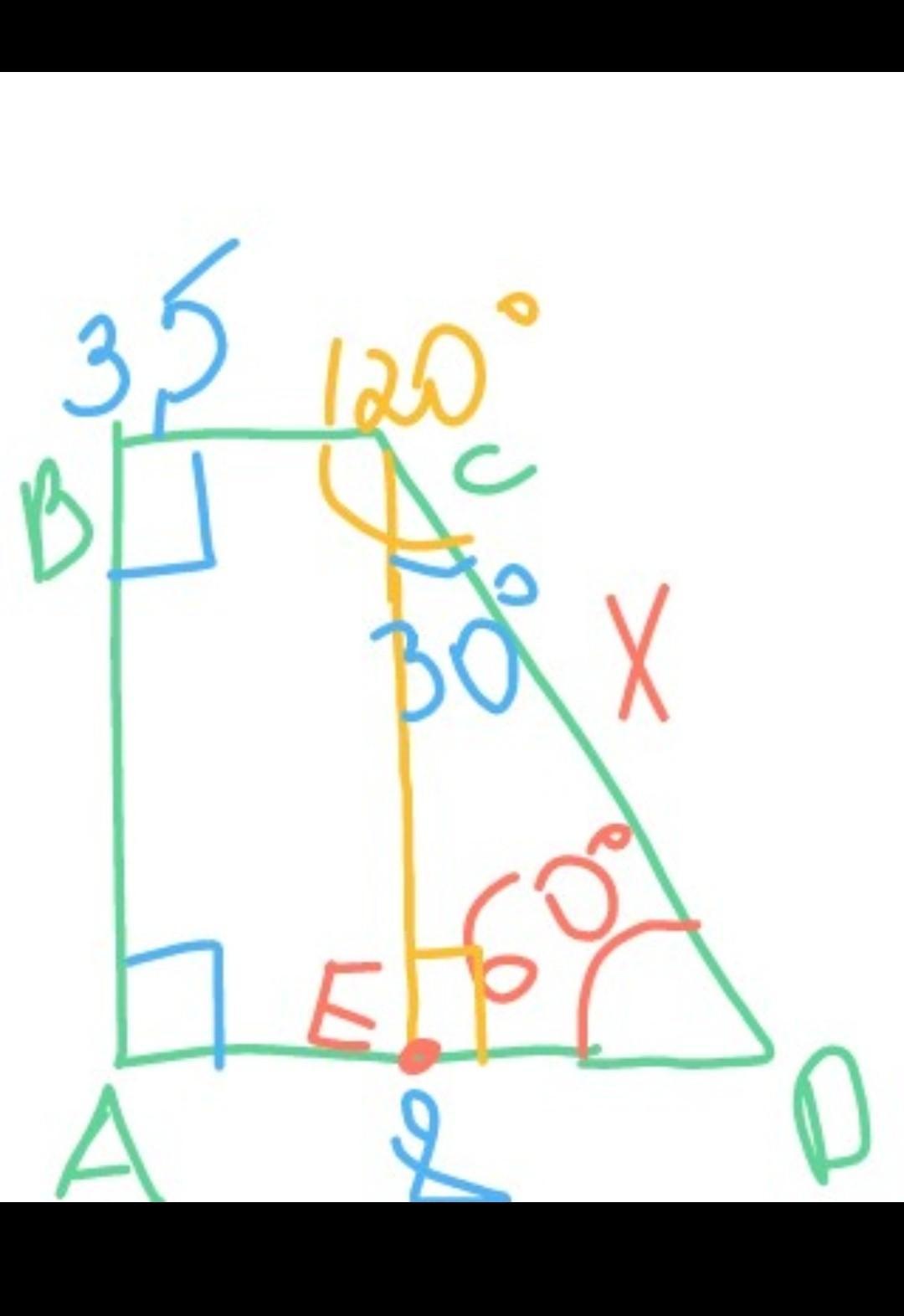
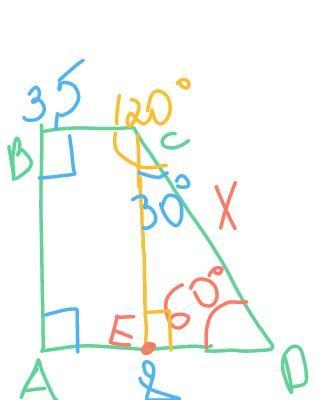Определи длину большей боковой стороны прямоугольной трапеции, если один из углов трапеции равен 60°, меньшее основание — 3,5 см, большее основание — 8 см.
Ответы
Ответ:
9см
Объяснение:
В четырехугольнике сумма всех углов равна 360 градусов, в этой трапеции два угла по 90 градусов и один по условию 60 = 90+90+60=240, третий угол = 360-240=120 градусов
Проведем перпендикуляр из угла С до основания большого (и еа большом основании отметим точку например Е)
Отрезок ЕD= большее основание минус меньшее, тоесть 8-3.5=4.5 см
Так же после проведения перпендикуляра к основанию получим треугольник СDE
В любом треугольнике сумма всех углов равна 180 градусов, один угол у нас по условию 60 градусов, один 90 так как перпендикуляр, тоесть третий угол в треугольнике равен 180-(90+60)=30 градусов
Ну и последнее, в треугольнике прямоугольном катет лежащий против угла в 30 градусов равен половине гипотенузы, так как наш катет равен 4.5 см (это отрезок ЕD), то гипотенуза равно 4,5*2=9 см это и есть наша большая Боковая сторона (СD)