Question

ГЕОМЕТРИЯ, 11 КЛАСС, 56 БАЛЛОВ

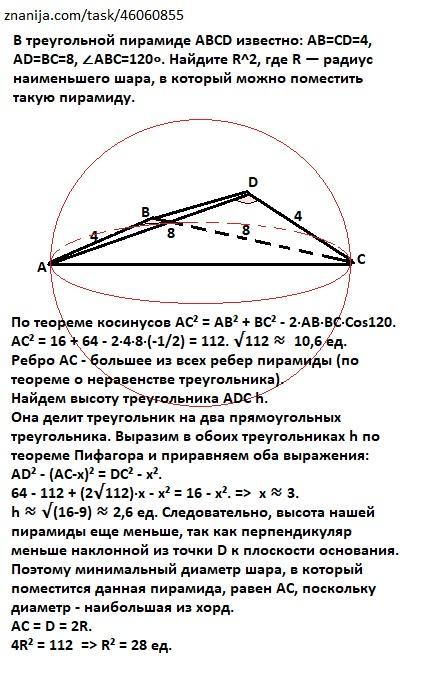
В треугольной пирамиде ABCD известно: AB=CD=4, AD=BC=8, ∠ABC=120∘. Найдите R^2, где R — радиус наименьшего шара, в который можно поместить такую пирамиду.

С простым или хотя-бы поверхностным пояснением, спасибо

Answer 1

Ответ:

R² = 28 ед.

Объяснение:

По теореме косинусов АС² = АВ² + ВС² - 2·АВ·ВС·Cos120.

АС² = 16 + 64 - 2·4·8·(-1/2) = 112. √112 ≈  10,6 ед.

Ребро АС - большее из всех ребер пирамиды (по теореме о неравенстве треугольника).

Найдем высоту треугольника ADC h.

Она делит треугольник на два прямоугольных треугольника. Выразим в обоих треугольниках h по теореме Пифагора и приравняем оба выражения:

AD² - (AC-x)² = DC² - x².

64 - 112 + (2√112)·x - x² = 16 - x². =>  x ≈ 3.

h ≈ √(16-9) ≈ 2,6 ед. Следовательно, высота нашей пирамиды еще меньше, так как перпендикуляр меньше наклонной из точки D к плоскости основания.

Поэтому минимальный диаметр шара, в который поместится данная пирамида, равен АС, поскольку диаметр - наибольшая из хорд.

AC = D = 2R.

4R² = 112  => R² = 28 ед.