Ответы
Объяснение:
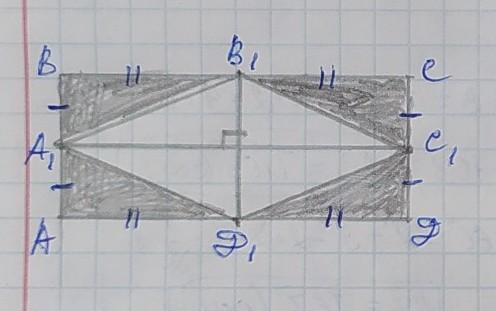
ДАНО: АВСД – прямоугольник, А₁∈ АВ;
В₁∈ ВС; С₁ ∈ СД; Д₁∈АД; АА₁=А₁В=СС₁=С₁Д; ВВ₁=В₁С=АД₁=Д₁Д.
ДОКАЗАТЬ: А₁В₁С₁Д₁ – ромб
ДОКАЗАТЕЛЬСТВО: треугольники А₁ВВ₁, В₁СС₁, С₁ДД₁ и АА₁Д₁ – прямоугольные и равны по первому признаку – двум катетам (по условию, согласно равенства сторон), поэтому А₁В₁=В₁С₁=С₁Д₁=А₁Д₁, следовательно четырёхугольник А₁В₁С₁Д₁ – равносторонний. Проведём его диагонали А₁С₁ и В₁Д₁. Так как точки А₁, В₁, С₁, Д₁ взяты с середин сторон прямоугольника АВСД, то:
А₁С₁ || ВС || АД; при этом А₁С₁=ВС=АД
В₁Д₁ || АВ || СД, аналогично: В₁Д₁=АВ=СД, а также диагонали также точкой пересечения делятся пополам, и так как стороны прямоугольника перпендикулярны и имеют разную величину, то и диагонали четырёхугольника так же будут перпендикулярны и разные по длине. Четырёхугольник А₁В₁С₁Д₁ имеет свойства ромба: все его стороны равны, диагонали имеют разную величину, пересекаются под прямым углом и точкой пересечения делятся пополам, следовательно
А₁В₁С₁Д₁ – ромб.
ДОКАЗАНО