Question

Точка О-центр окружности. Чему равно значение угла x в градусах?​

Answer 1

Ответ:

68°

Объяснение:

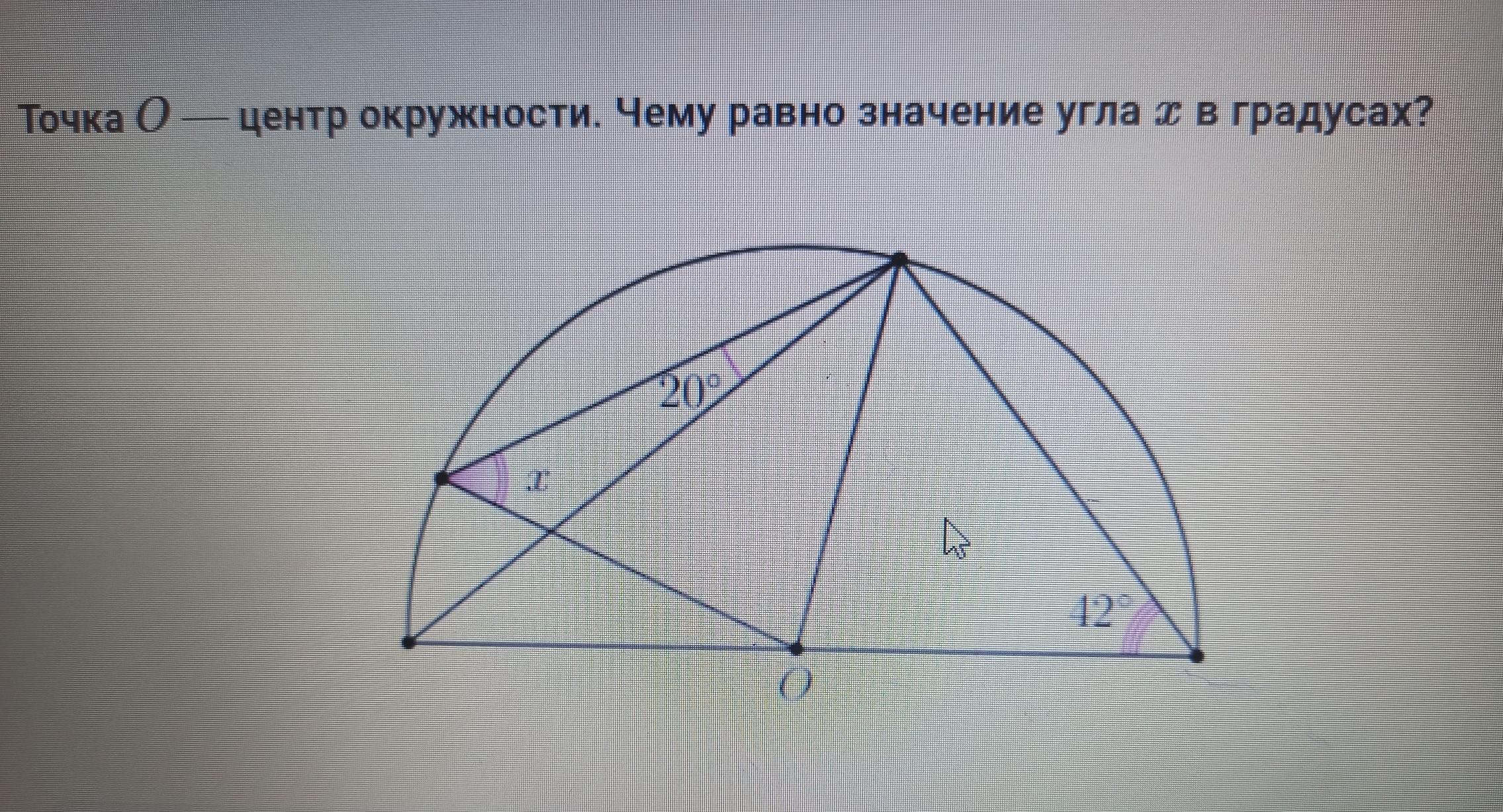
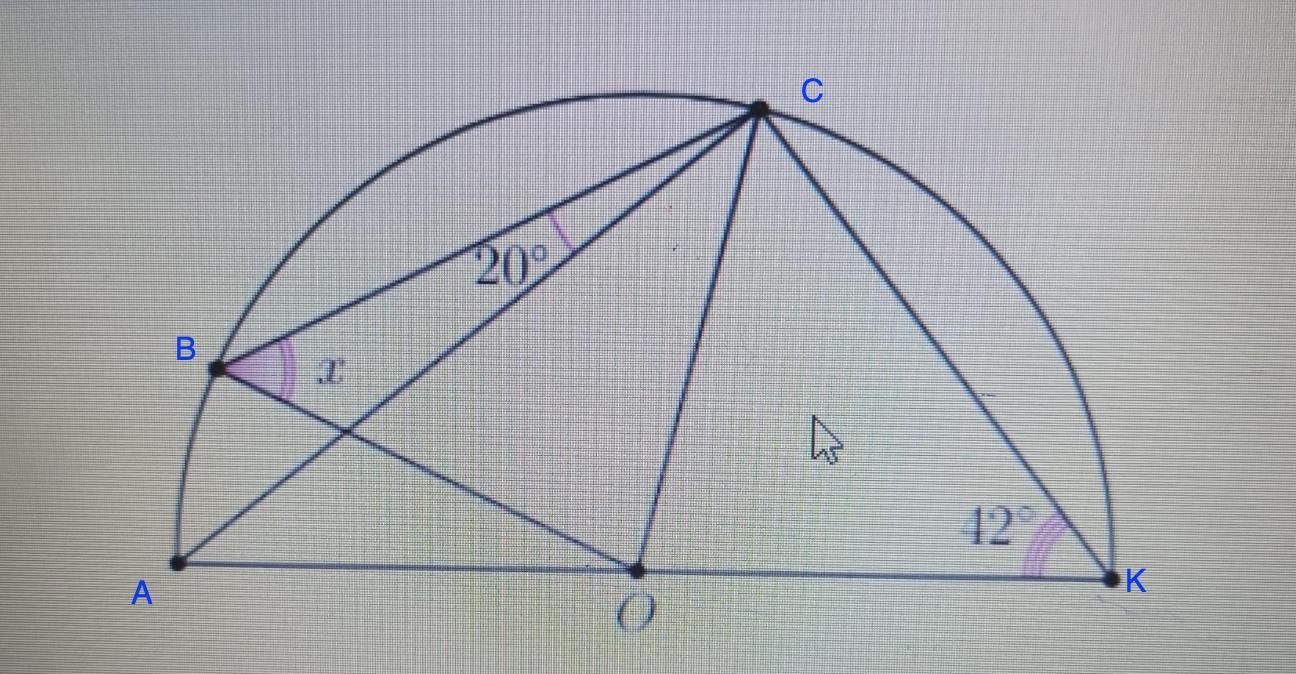
Дано: полуокружность О; АО.

∠АСВ=20°; ∠АКС=42°

Найти: ∠ОВС

Решение:

• Вписанный угол равен половине дуги, на которую он опирается.

⇒ ∪ АВ=2·∠АСВ=20°·2=40° (вписанный)

∪ АВС = 2·∠АКС=42°·2=84°

Тогда ∪ ВС= ∪АВС - ∪ АВ = 84°-40°=44°

• Центральный угол равен дуге, на которую он опирается.

⇒ ∠ВОС=∪ ВС = 44°

ΔВОС - равнобедренный,

ОВ=ОС=R.

⇒∠ОВС=∠ОСВ (при основании р/б треугольника)

• Сумма углов треугольника равна 180°.

⇒∠ОВС=∠ОСВ=(180°-∠ВОС) : 2=(180°-44°) : 2=68°