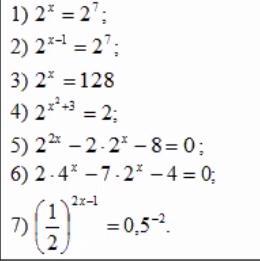Ответы
Ответ дал:
0
Пошаговое объяснение:
корней нет
квадратное показательное уравнение, замена переменной:
обратная замена:
посторонний корень (t>0)
квадратное показательное уравнение, замена переменной:
t1=(-1/2) посторонний корень (t>0)
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
8 лет назад
8 лет назад
9 лет назад