Question

№ 1
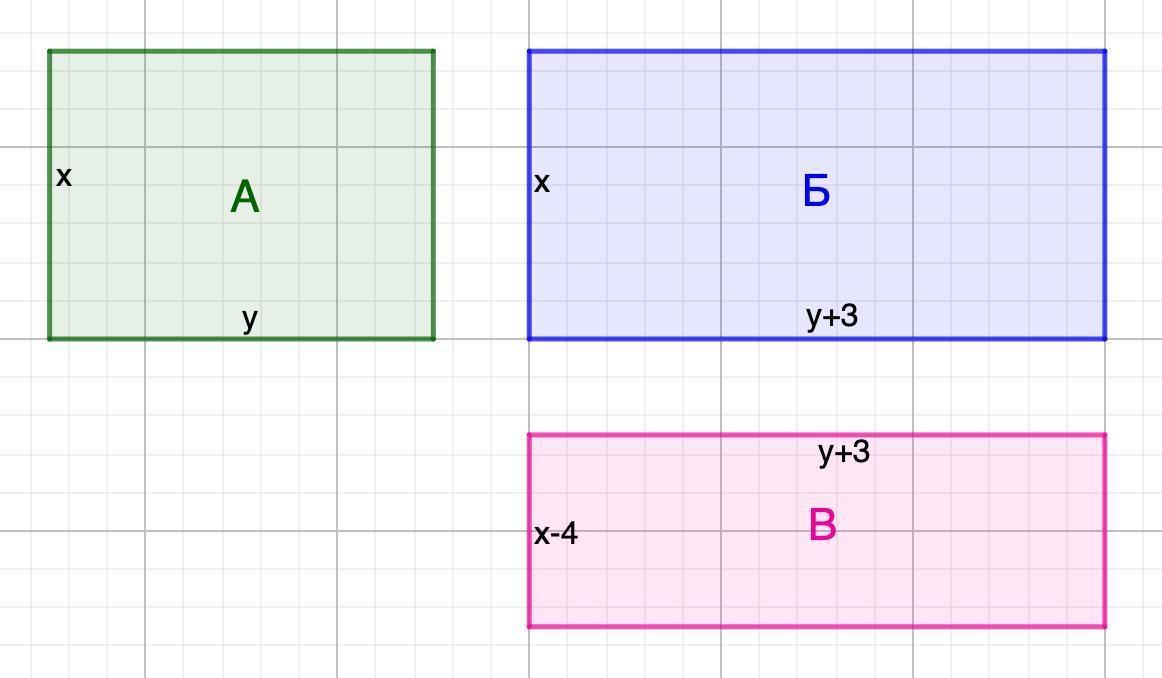
На листе нарисованы три прямоугольника А, Б и В.

У прямоугольников А и Б одинаковая ширина, а у прямоугольников Б и В одинаковая длина (ширина — сверху вниз, длина — слева направо). Длина прямоугольника Б больше длины прямоугольника А на 3 см, и площадь Б больше площади А на 33 см2. Ширина прямоугольника В меньше ширины прямоугольника Б на 4 см, и площадь В меньше площади Б на 52 см2. Найдите площадь прямоугольника А в квадратных сантиметрах.

Answer 1

Ответ:

Пошаговое объяснение:

Даны три прямоугольника: А, Б, В.

Пусть ширина и длина прямоугольника А равны х и у соответственно.

Тогда в прямоугольнике Б ширина равна х, а длина больше длины прямоугольника А на 3 см, то есть (у+3) (см).

В прямоугольнике В длина равна длине прямоугольника Б, то есть (у+3) (см).

Ширина прямоугольника В меньше ширины прямоугольника Б на 4 см и равна (х-4) (см).

Площадь прямоугольника находим по формуле:

• S=ah, где а - ширина, h - высота.

⇒ S(А)=ху (см²);

S(Б)=х(у+3)=(ху+3х) (см²)

S(В)=(х-4)(у+3)=(ху+3х-4у-12) (см²)

Известно, что

1) S(Б)-S(A)=33 (см²)

2) S(Б)-S(В)=52 (см²)

или

1) (ху+3х)-ху=33

3х=33

х=11

Ширина прямоугольника А - 11 см.

2) (ху+3х)-(ху+3х-4у-12)=52

ху+3х-ху-3х+4у+12=52

4у=40

у=10

Длина прямоугольника А - 10 см.

Тогда площадь прямоугольника А:

S(A)=11·10=110 (см²)