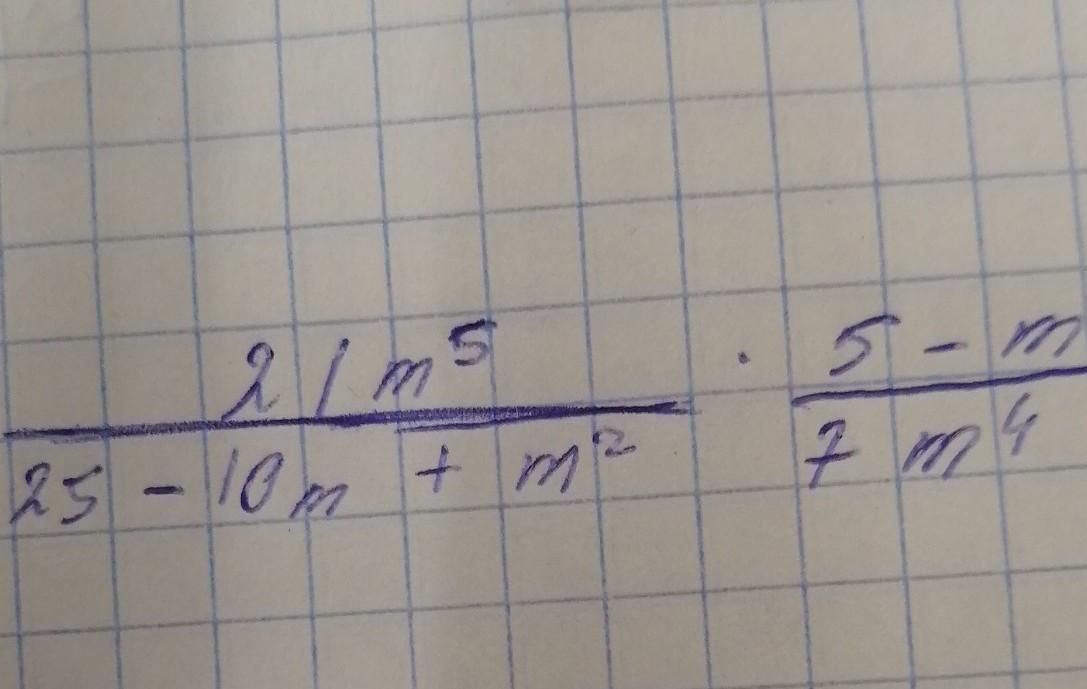Ответы
Ответ дал:
0
Выражение:
Знаменатель первой дроби можно свернуть по формуле квадрата суммы:
Тогда:
Между прочим, запись абсолютно равноценна записи
, поэтому можно использовать либо первую, либо вторую форму для дальнейшего решения этого выражения. Нам удобнее взять первую:
Теперь:
- сокращаем числитель первой дроби и знаменатель второй дроби на ;
- сокращаем знаменатель первой дроби и числитель второй дроби на скобку (5-m);
Получаем:
Если численного значения переменной "m" не дано, то на этом преобразования закончены.
Ответ:
Вас заинтересует
3 года назад
8 лет назад
8 лет назад