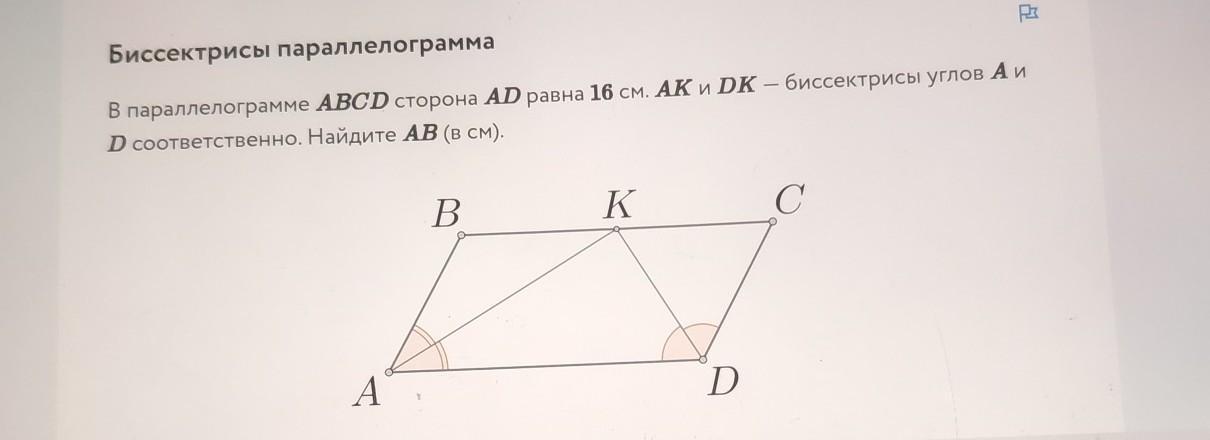
В параллелограмме ABCD сторона AD равна 16 см. АК и DK – биссектрисы углов А и D соответственно. Найдите AB (в см)
Приложения:
Ответы
Ответ дал:
2
Ответ: 8
Объяснение:
∠DKC=∠KDA (накрест лежащие секущей KD пересекающей параллельные прямые BC и AD)
А по условию ∠KDA=∠KDC (DK - биссектриса)
Следовательно ΔKDC равнобедренный и KC=CD
∠BKA=∠KAD (накрест лежащие секущей AK пересекающей параллельные прямые BC и AD)
А по условию ∠KAD=∠KAB (AK - биссектриса)
Следовательно ΔABK равнобедренный и BK=AB
В параллелограмме противоположные стороны равны и AB=CD, откуда следует, что и BK=KC.
Следовательно
Вас заинтересует
2 года назад
2 года назад
3 года назад
8 лет назад
9 лет назад