Доведіть, що коли бісектриси кутів АВС і СВD перпендикулярні, то точки А, В і D лежать на одній прямій.
Ответы
Ответ дал:
2
Ответ:
я не знаю украинский, но надеюсь ты знаешь русский
1. биссектрисы смежных углов взаимно перпендикулярны, тогда
∠АВД = 180° - развернутый, т.е прямая линия.
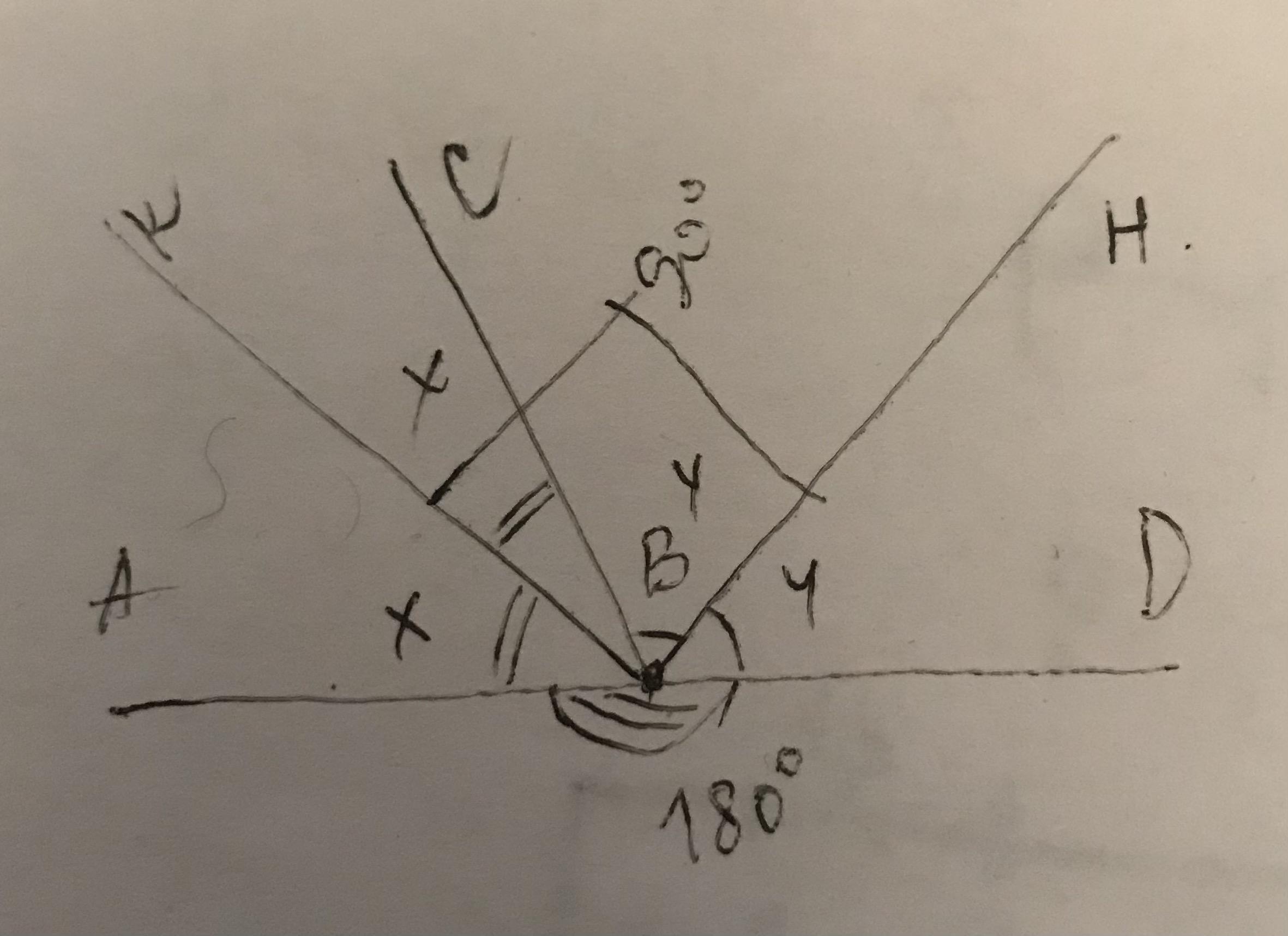
2. ВК - биссектриса ∠АВС, ВН - биссектриса ∠СВД, ∠KВН = 90°, ∠АВК=∠КВС = х
∠СВН=∠НВД = у,
∠КВС+∠СВН = х+у = 90°
∠АВК+∠НВД = х+у = 90°
∠АВД = 90+90 = 180° - развернутый угол - прямая
на всякий случай см рисунок
Объяснение:
Приложения:
Вас заинтересует
2 года назад
2 года назад
3 года назад
8 лет назад
8 лет назад
10 лет назад