В равнобокой трапеции один из углов равен 120°, диагональ трапеции образует с основанием угол 30°. Найдите основания трапеции, если ее боковая сторона равна 8 см.
Приложения:
Аноним:
8; 16.
Ответы
Ответ дал:
1
Ответ:
8 см 16 см
Объяснение:
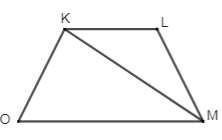
Дано: ОКLM - трапеция; OK=LM=8 см; КM - диагональ; ∠KMO=30°; ∠L=120°. Найти МO и КL.
∠OМК=∠LКM как внутренние накрест лежащие при KL║OM и секущей КM.
∠KML=180-120-30=30°
ΔКLМ - равнобедренный, KL=ML=8 см.
ΔОКМ - прямоугольный; ∠ОКМ=120-30=90°;
ОМ=2*ОК=8*2=16 см по свойству катета, лежащего против угла 30°.
Вас заинтересует
2 года назад
3 года назад
8 лет назад
8 лет назад
9 лет назад