найдите множество точек координатной плоскости, которое задано системой неравенств:
y≥x^2-4
(x+1)^2+(y+2)^2≤4
Simba2017:
это парабола и окружность
не гипербола разве?
у гиперболы х в знаменателе
да, я перепутала. Извините.
вам ответ понятен?
да, спасибо
какие тут точки?!?
Ответы
Ответ дал:
6
строю параболу y=x^2-4
x0=-b/(2a)=0
y0=y(x0)=y(0)=-4
(0;-4)-вершина параболы
y(-2)=(-2)^2-4=0
y(2)=2^2-4=0
нули функции у (-2;0);(2;0)
решением неравенства y≥x^2-4 будет внутренняя область параболы, включая саму параболу
(x+1)^2+(x+2)^2=4-уравнение окружности с центром (-1;-2) и радиуса 2
решением неравенства (x+1)^2+(y+2)^2≤4 будет сама окружность и вся ее внутренняя область
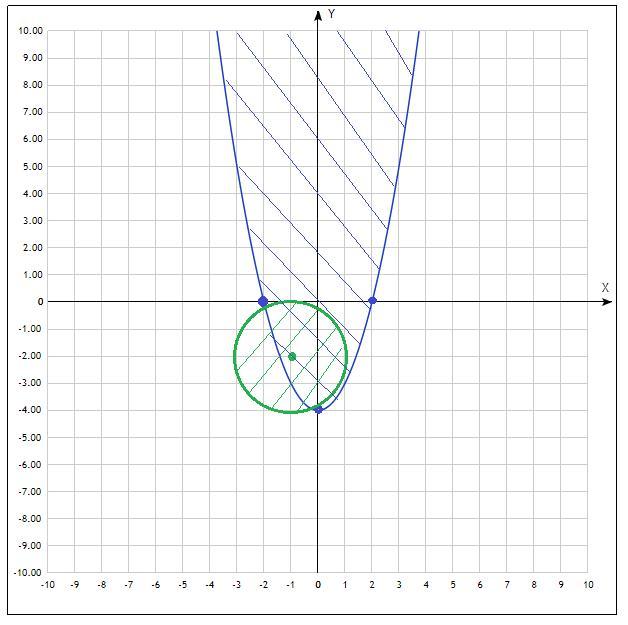
решением системы будет пересечение областей параболы с ее внутренней областью и окружности с его внутренней областью
Ответом будет область, где двойная штриховка-представлена на рисунке
Приложения:
какие тут точки?!?
мне нужно хотя бы обозначить где и какая координата
вы не понимаете ответа?
не ну можешь написать как ты до этого додумался
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
8 лет назад
9 лет назад