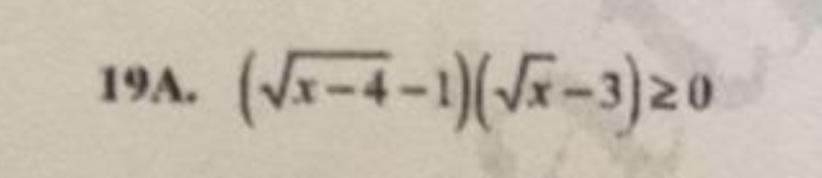Ответы
Ответ дал:
1
Объяснение:(×
≥0
Х∈ [ 4, +∞⟩
∫≥0
∫√x-3≥0
∫√x-4-1≤0
∫√x-3≤0
∫x≥5
∫x≥9
∫x≤5
∫x≤9
x∈ [ 9, +∞⟩
x∈ ⟨-∞,5]
x∈ ⟨-∞,5]∪[ 9, +∞⟩, x∈ [ 4,+∞⟩
x∈[4,5] ∪[ 9, +∞⟩
Ответ дал:
1
Объяснение:
ОДЗ:
Найдём значения х, при которых множители равны нулю:
-∞__+__5__-__9__+__+∞ ⇒
х∈(-∞:5]U[9;+∞).
Согласно ОДЗ:
Ответ: х∈[4;5]U[9;+∞).
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
8 лет назад
10 лет назад