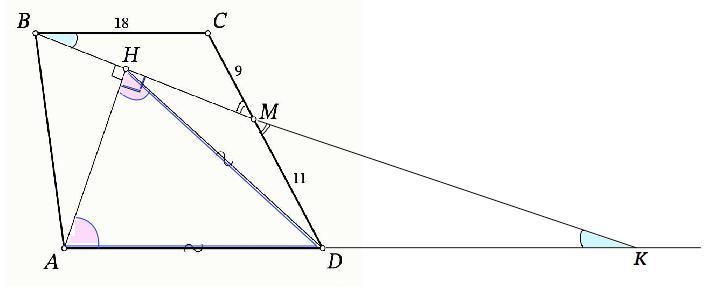
На боковой стороне CD трапеции ABCD (AD∥BC) отмечена точка M.
Из вершины A на отрезок BM опущен перпендикуляр AH. Оказалось, что AD=HD.
Найдите длину отрезка AD, если известно, что BC=18, CM=9, MD=11.
Ответы
Ответ дал:
5
Ответ: 22 ( ед. длины)
Объяснение:
Продлим ВМ до пересечения с продолжением АD в точке К. ∠СВМ=∠DKM ( накрестлежащие при ВС║АК и секущей ВК), вертикальные углы при М равны .⇒ ∆ ВСМ подобен ∆ КDM по 1-му признаку (по двум углам).
Из подобия треугольников следует отношение СМ:МD=BC:DK ⇒
DK=MD•BC:CM
DK=11•18:9=22.
Рассмотрим ∆ АНК. ∠АНD+∠KHD=90° .
Из суммы острых углов прямоугольного треугольника ∠НАК+∠AKН=90°
Но ∠НАК=∠АHD ⇒ ∠КНD=∠НКD ⇒ ∆ KHD – равнобедренный.
HD=KD=22. ⇒
АD=HD=22. (ед. длины)..
Приложения:
BlackFox2030:
здравствуйте! можете пожалуйста помочь с геометрией
Вас заинтересует
2 года назад
3 года назад
3 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад