Ответы
Ответ дал:
1
Ответ:
120 см
Объяснение:
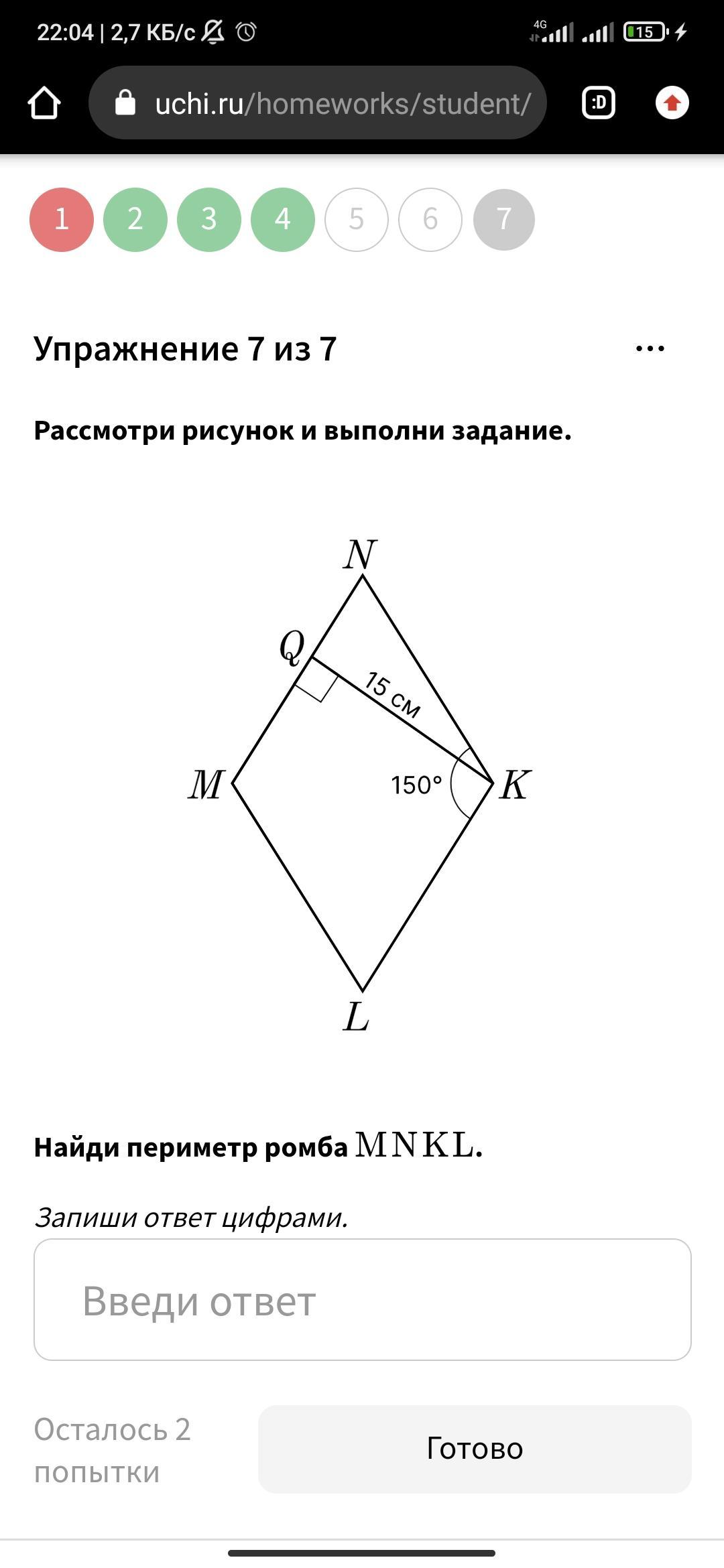
Дано: MNKL - ромб;
KQ⊥MN
∠K=150°
KQ=15 см
Найти: Р (MNKL)
Решение:
- Если отрезок перпендикулярен одной из параллельных прямых, то он перпендикулярен и к второй прямой.
⇒ KQ⊥LK ⇒∠QKL=90°
Рассмотрим ΔQNK - прямоугольный.
∠QKN=∠K-∠QKL=150°-90°=60°
- Сумма острых углов прямоугольного треугольника равна 90°.
⇒ ∠N=90°-∠QKN=90°-60°=30°
- Катет, лежащий против угла в 30°, равен половине гипотенузы.
⇒ NK=2·KQ=15·2=30 (см)
- Периметр - сумма длин всех сторон.
Так как у ромба все стороны равны, то периметр равен:
Р (MNKL)=30·4=120 (см)
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
8 лет назад
8 лет назад