Question

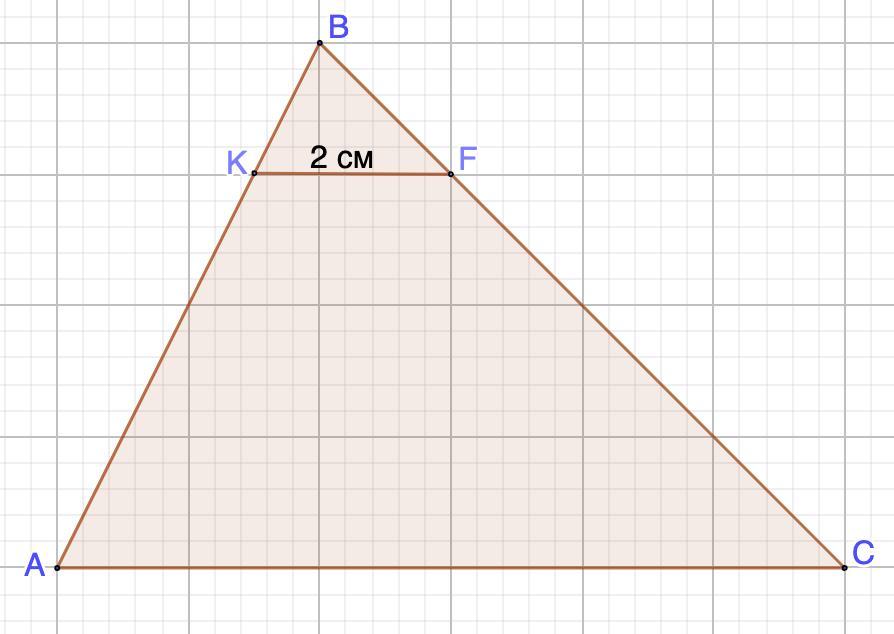
На сторонах АВ и ВС треугольника АВС отметили соответственно точки К и F так, что АВ = 4BK, BC = 4BF. Найдите сторону АС, если KF = 2 см. Я не понимаю как эту задачу решить. Помогите пожалуйста

Answer 1

Ответ:

АС=8 см

Объяснение:

Дано: ΔАВС;

АВ = 4BK, BC = 4BF;

KF = 2 см

Найти: АС

Решение:

Рассмотрим ΔKBF и ΔАВС.

∠В - общий.

AВ = 4BK или

$\displaystyle \frac{AB}{BK}=\frac{4}{1}$

BC = 4BF  или

$\displaystyle \frac{BC}{BF}=\frac{4}{1}$

⇒ ΔKBF ~ ΔАВС (по двум пропорциональным сторонам и углу между ними)

$\displaystyle \frac{AC}{KF}=\frac{4}{1} \\\\\Rightarrow AC=4KF=2*4=8$

АС=8 см

Если подобие не проходили, то можно решить так:

Проведем среднюю линию MN.

1. АВ = 4BK

Пусть ВК=х, тогда АВ=4х.

2. BC = 4BF

Пусть BF=у, тогда ВС=4у

3. MN - средняя линия ΔАВС ⇒ АМ=МВ=2х; BN=NC=2у.

4. Рассмотрим ΔMBN.

BK=x ⇒ KM=BM-BK=2x-x=x

BF=y ⇒ FN=BN-BF=2y-y=y

⇒ KF - средняя линия ΔMBN.

• Средняя линия треугольника параллельна третьей стороне и равна ее половине.

⇒ MN=2*2=4 (см)

5. MN - средняя линия ΔАВС

⇒ АС=4*2=8 (см)