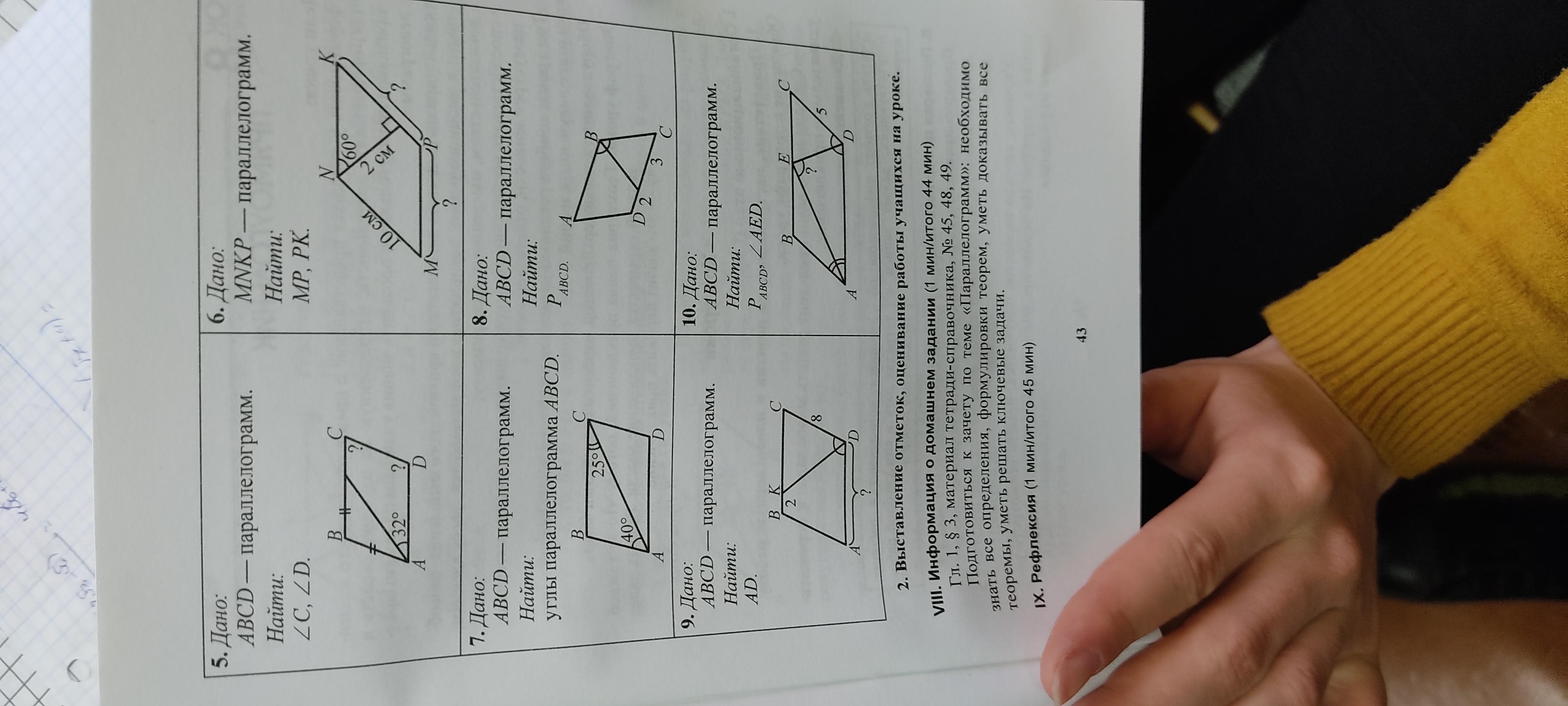
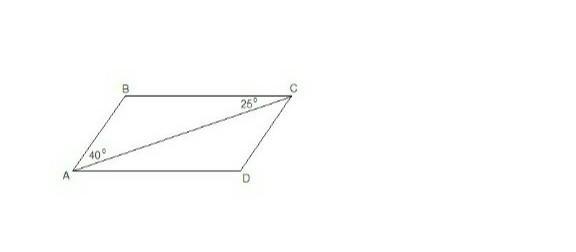
ABCD- параллелограмм, AC- диагональ,
Угол BAC- 40 градусов, угол BCA- 25 градусов, найти: все углы параллелограмма (зад.7)
Приложения:
Ответы
Ответ дал:
0
Ответ:
Тут все легко
ВС И АDпаралельны, АС-секущая, следовательно угол BAC=ABD=40 грлвсам как накрест ледащие( по моему или какие то другие), а уголы BCA=CAD=25 градусов.
Их сумма равна 65+65=130 градусов.
Сделовательно остальные 2 унла равны:
180-130=50
50/2=25
Угол B=D=25градусов
Можно в лучший ответ, я старалась))
Ответ дал:
0
Ответ:
️АВС: <АВС=180⁰-(<ВАС+<ВСА)=180⁰-(40°+25)=115⁰
В параллелограмме противолежащие углы равны, значит
<АDC=<АВС=115°
сумма углов прилежащих к одной стороне параллелограмма, равна 180°.
<ВАD=180°-<AВС=180°- 115°=65°
Ответ:65°,65°,115°,115°
Приложения:
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
8 лет назад
10 лет назад