Question

Решите елементарную задачу по геометрии, желательно с объяснентем))​

Answer 1

Ответ:

$\frac{8\sqrt{2}}{3}$

Объяснение:

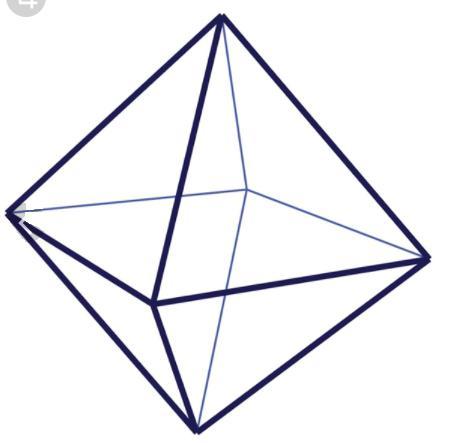
Правильный октаэдр можно представить как две пирамиды, соответственно его объем будет равен удвоенному объему одной из пирамид.

Объем пирамиды можно найти по формуле $V'=\frac{1}{3}a^{2}h$, где a-длина ребра октаэдра, а h - высота пирамиды.

Найдем ее как высоту в треугольнике образованном двумя противоположными ребрами пирамидами и диагональю основания проведенной между ними. Тогда две стороны этого равнобедренного треугольника равны a, а третья $a\sqrt{2}$, как диагональ квадрата со стороной a.

Тогда высота найдется из прямоугольного треугольника, в котором она является катетом, ребро пирамиды гипотенузой, а половина диагонали вторым катетом:

$h=\sqrt{a^{2}-(\frac{a\sqrt{2}}{2})^{2}}=\frac{a}{\sqrt{2}}$

Для объема октаэдра получим общую формулу $V=2V'=\frac{2}{3}a^{2}*\frac{a}{\sqrt{2}}=\frac{\sqrt{2}}{3}a^{3}$

Для заданного в задаче ребра $V=\frac{\sqrt{2}}{3}*2^{3}=\frac{8\sqrt{2}}{3}$