Ответы
Ответ дал:
0
решениееееееееееееееееееееееееееееееееееее
Приложения:

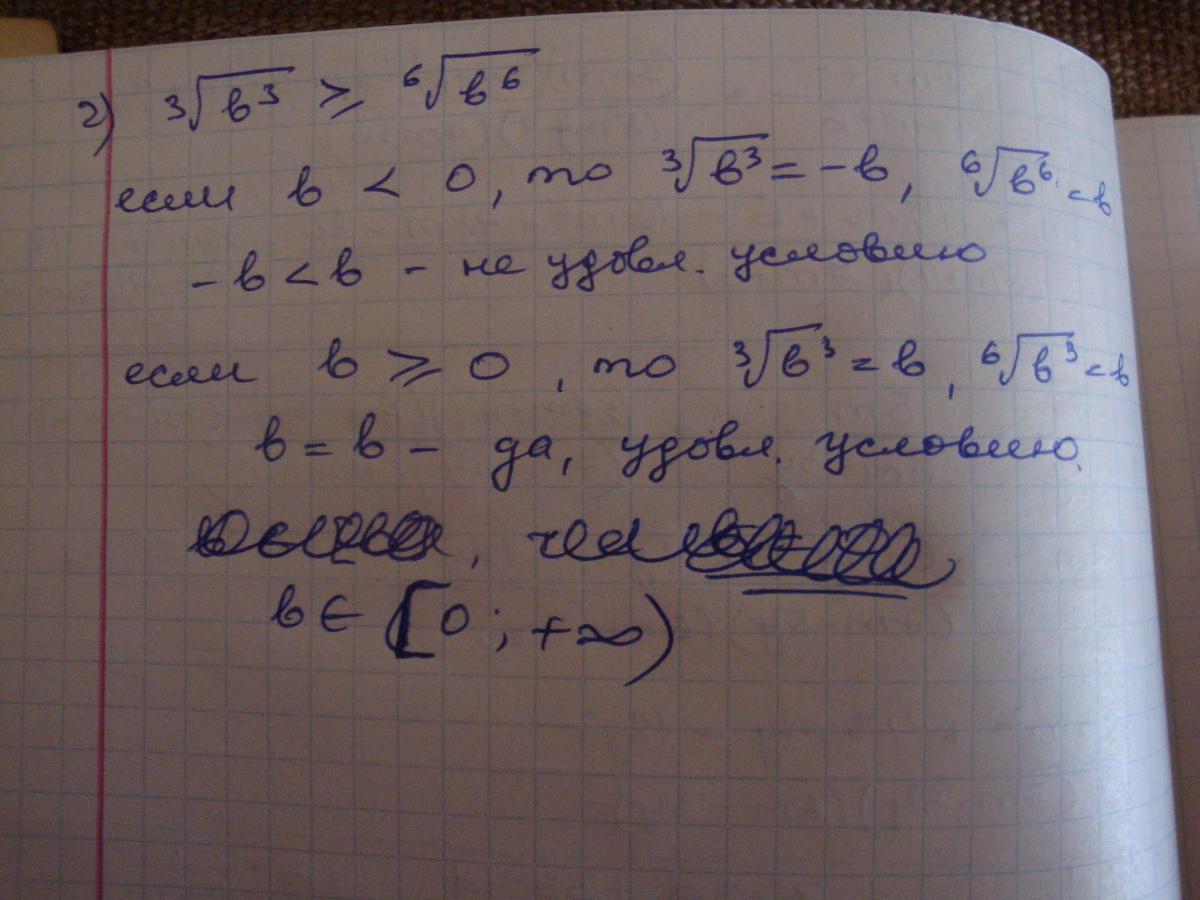
Ответ дал:
0
так оно и есть
Вы не забывайте и пользуйтесь модулями если проходили
модули появляются в четых степених при решениях и в корнях четной степени
Вам надо решить два уравнения
![sqrt[3]{b^3}<= sqrt[6]{b^6} \ b<=!b! sqrt[3]{b^3}<= sqrt[6]{b^6} \ b<=!b!](https://tex.z-dn.net/?f=+sqrt%5B3%5D%7Bb%5E3%7D%26lt%3B%3D+sqrt%5B6%5D%7Bb%5E6%7D+%5C+b%26lt%3B%3D%21b%21++)
это выполняется всегда
![sqrt[3]{b^3}>= sqrt[6]{b^6} \ b>=!b! sqrt[3]{b^3}>= sqrt[6]{b^6} \ b>=!b!](https://tex.z-dn.net/?f=+sqrt%5B3%5D%7Bb%5E3%7D%26gt%3B%3D+sqrt%5B6%5D%7Bb%5E6%7D+%5C+b%26gt%3B%3D%21b%21++)
это только при положительных и равных 0
------------------------------------------
тоже самое при степения
![x^{2n}=A \ !x!= sqrt[2n]{A} \ x^{2n+1}=B \ x= sqrt[2n+1]{B} x^{2n}=A \ !x!= sqrt[2n]{A} \ x^{2n+1}=B \ x= sqrt[2n+1]{B}](https://tex.z-dn.net/?f=x%5E%7B2n%7D%3DA+%5C+%21x%21%3D++sqrt%5B2n%5D%7BA%7D++%5C+x%5E%7B2n%2B1%7D%3DB+%5C+x%3D+sqrt%5B2n%2B1%5D%7BB%7D+)
Вы не забывайте и пользуйтесь модулями если проходили
модули появляются в четых степених при решениях и в корнях четной степени
Вам надо решить два уравнения
это выполняется всегда
это только при положительных и равных 0
------------------------------------------
тоже самое при степения
Приложения:

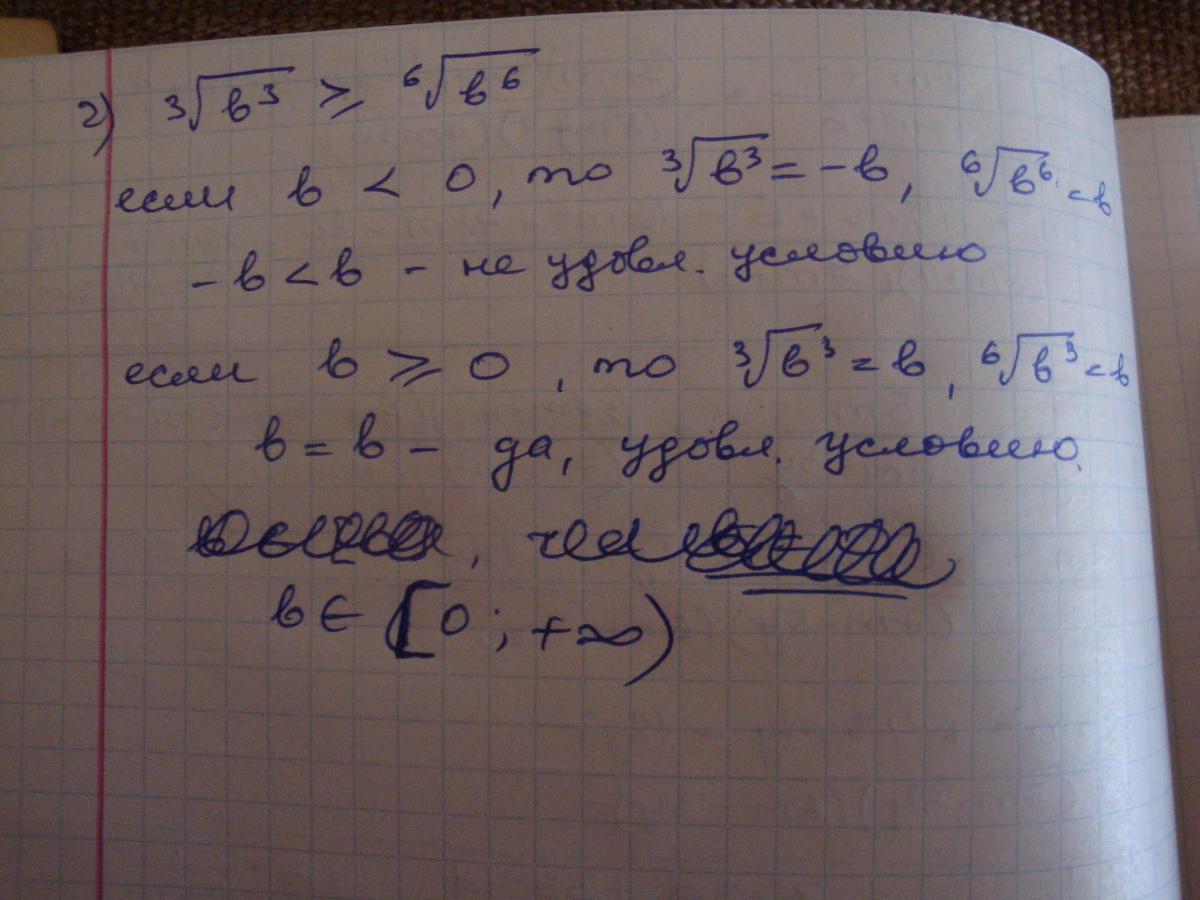
Ответ дал:
0
Спасибо
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад
11 лет назад
