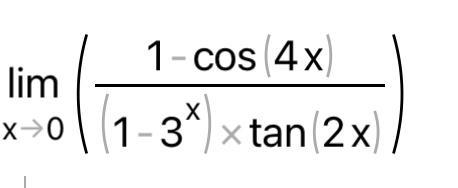Ответы
Ответ дал:
1
Пользуясь таблицей эквивалентных бесконечно малых функций (x→0),
,
,
, получим
dareovan:
спасибо большое
Вас заинтересует
2 года назад
3 года назад
3 года назад
8 лет назад
8 лет назад
9 лет назад