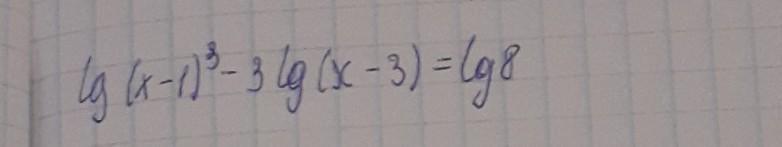Ответы
Ответ дал:
0
Ответ:
х=5
Пошаговое объяснение:
ОДЗ:
С учетом свойств логарифма при равенстве логарифмов с одним основанием подлогарифмические выражения также равны (если определены). Запишем:
Следовательно х=5 - является корнем уравнения.
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
8 лет назад
8 лет назад
9 лет назад