Question

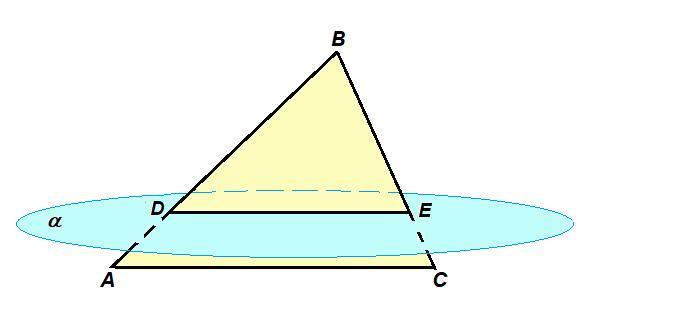
Дано трикутник ABC. Площина а
, яка
паралельна стороні AC, перетинає сторону
AB трикутника в точці D , а сторону BC–в
точці E. Обчисліть DE , якщо BE:BC=4:5,
AC=15 см.

Answer 1

Ответ:

DE = 12 см

Объяснение:

Если плоскость проходит через прямую, параллельную другой плоскости и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.

АС║α, плоскость (АВС) проходит через АС и пересекает плоскость α по прямой DE, значит DE║AC.

Прямая, параллельная стороне треугольника, отсекает от него треугольник, подобный данному, значит

ΔDBE ~ ΔABC.

$\dfrac{DE}{AC}=\dfrac{BE}{BC}$

$\dfrac{DE}{15}=\dfrac{4}{5}$

$\boldsymbol{DE}=\dfrac{4\cdot 15}{5}=4\cdot 3\boldsymbol{=12}$ см