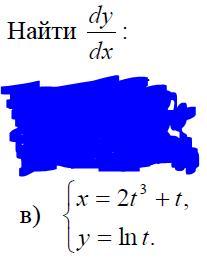Ответы
Ответ дал:
2
Производная функции, заданной параметрически:
Находим производную:
Аноним:
точно
Вас заинтересует
2 года назад
3 года назад
3 года назад
8 лет назад
9 лет назад
9 лет назад