Question

ПОМОГИТЕ, ПОЖАЛУЙСТА, СРОЧНО!! ДАЮ 20 БАЛЛОВ

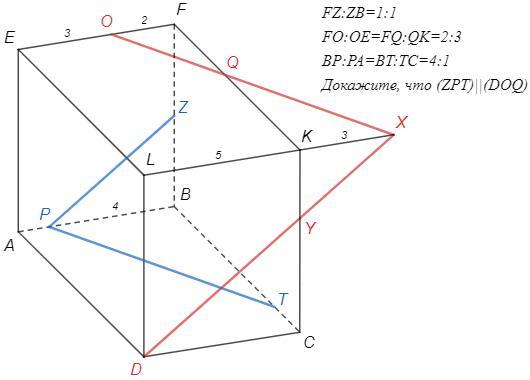
Дан прямоугольный параллелепипед ABCDEFKL, где Z - середина FB, а на ребрах FE и FK, точки O и Q соответственно делят эти ребра в отношении 2:3, считая от вершины F, а на ребрах BA и BC отмечены точки P и T соответственно в отношении 4:1, считая от вершины B. Докажите, что плоскость, которой принадлежат точки Z, P, T, параллельна плоскости, содержащей точки D, O, Q.

Answer 1

Если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости, то плоскости параллельны.

Докажем PT||OQ

PT и OQ лежат в параллельных гранях.

Достаточно доказать, что они образуют равные углы с ребрами AB и EF.

FO/BP =FQ/BT =2/4 => △PBT~△OFQ (по двум пропорциональным сторонам и углу между ними)

∠BPT=∠FOQ => PT||OQ

OQ пересекает LK в точке X.

DX пересекает CK в точке Y.

Аналогично докажем PZ||DX

△OFQ~△XKQ => OF/XK =FQ/QK =2/3 => XK/EF =3/5

XL/PB =8/4 =LD/ZB => △XLD~△PBZ

∠BPZ=∠LXD=∠CDX => PZ||DX

PT||OX, PZ||DX => (ZPT)||(DOQ)