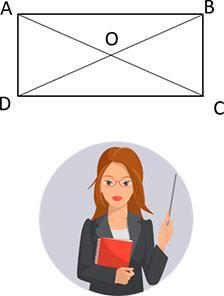
Пусть ABCD – прямоугольник, диагонали AC и BD пересекаются в точке O. Найдите периметр треугольника AOD, если угол ACD = 30°, АС = 54 см.
Приложения:
Ответы
Ответ дал:
0
Ответ:
81 см
Объяснение:
В прямоугольники диагонали равны и точкой пересечения делятся пополам. Поэтому АС= BD=54 cм и АО=OD=54:2=27 см
Так как ABCD – прямоугольник, значит ∠ADC=90°, поэтому ΔADC-прямоугольный с гипотенузой АС, а катет AD лежит против
∠ACD = 30°, значит AD=AC=27 cм
периметр треугольника AOD=AO+OD+AD=27+27+27=81 см
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
8 лет назад
8 лет назад
10 лет назад