Ответы
Ответ дал:
0
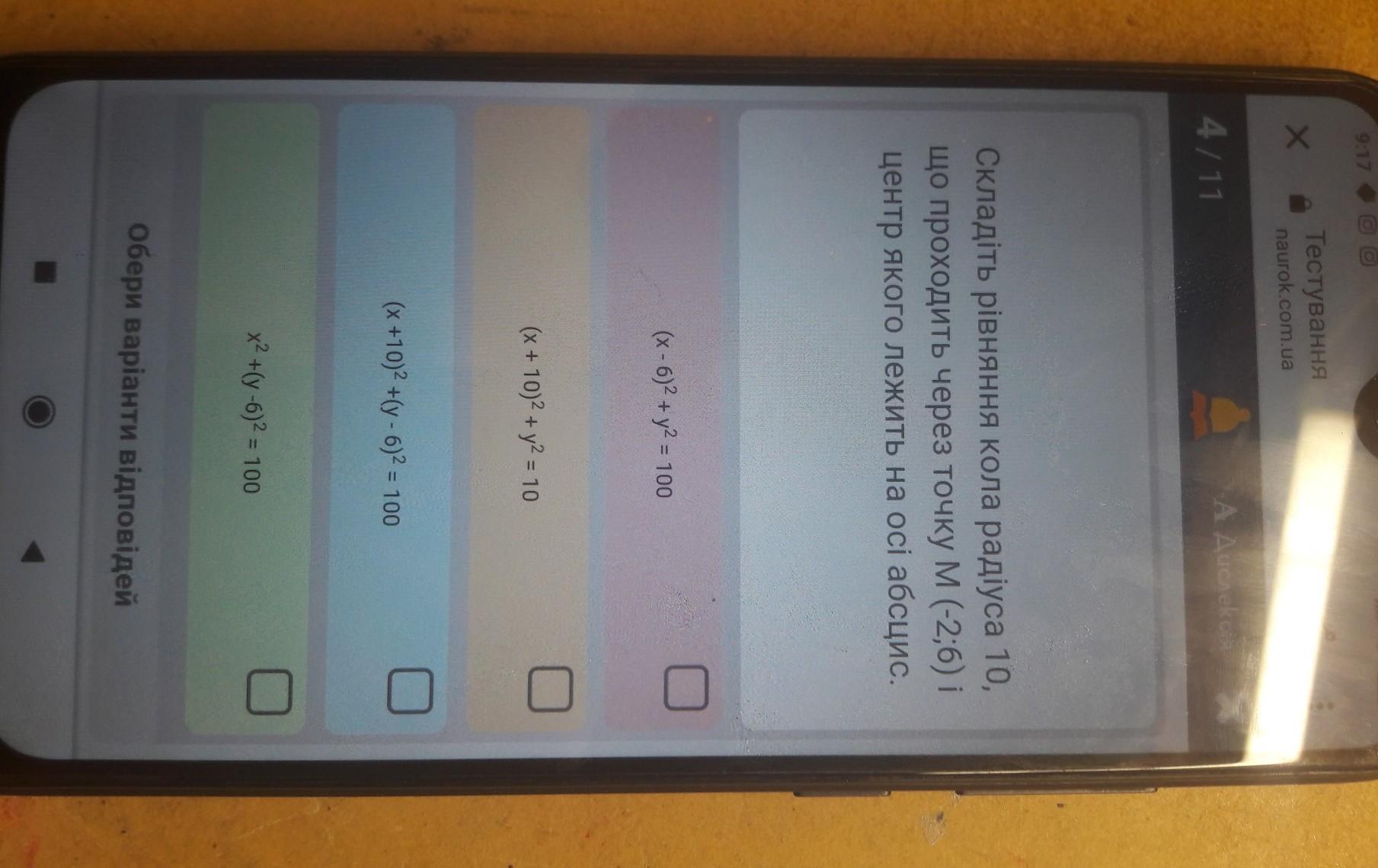
Уравнение окружности с радиусом R:
- координаты центра
Из условия:
Таким образом:
Методом исключения, подходит только вариант 1). Докажем это.
Подставим точку M (-2;6) и решим уравнение относительно x₀
По теореме Виета:
Ответ:
[есть в вариантах]
[нет в вариантах]
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
10 лет назад