Question

Решение неравенств с двумя переменными и их систем.

а) (x-3)(5х-4)(8-х)$\geq 0$
б) (х+8)(3-х)(1,5-х)<0;
в) 4(х+3) (х-2)>0

Answer 1

а) найдём нули функции

$(x-3)(5x-4)(8-x)\geq 0\\{}\quad\ 3\qquad\ 0.8\qquad\ 8$

Отмечаем на координатной прямой (см. приложение 1) – неравенство нестрогое, точки включаются в значение

Проставляем знаки:

++- = -

Ответ:  $x\in(-\infty;\ 0.8]\cup[3;\ 8]$

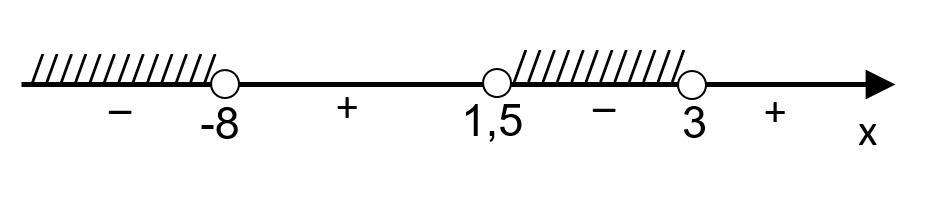
б) нули функции:

$(x+8)(3-x)(1.5-x)<0\\{}\ -8\qquad\ 3\qquad\, \ 1.5$

(приложение 2) – неравенство строгое, точки выколоты

Проставляем знаки:

+-- = +

Ответ:  $x\in(-\infty;\ -8)\cup(1.5;\ 3)$

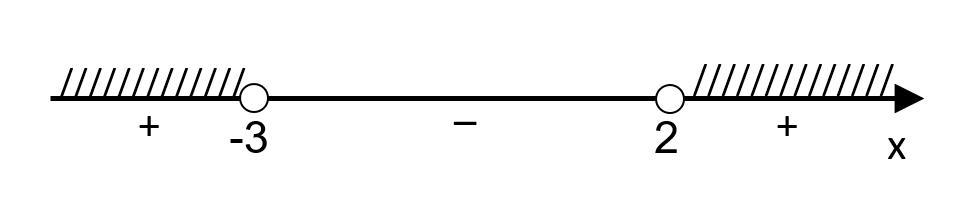
в) нули функции:

$4(x+3)(x-2)>0\\{}\ \ \,-3\qquad \ 2$

(приложение 3) – неравенство строгое, точки выколоты

Проставляем знаки:

++ = +

Ответ: $x\in(-\infty;\ 3)\cup(2;\ +\infty)$