СРОЧНО
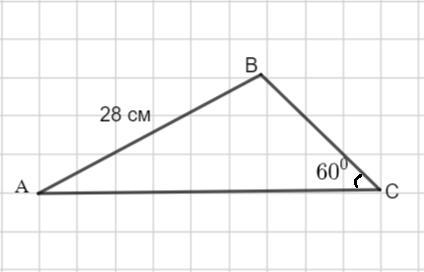
Разность двух сторон треугольников равна 20 см, а угол между ними равен 60° Найдите меньшую из этих сторон если третья сторона равна 28см
Ответы
Ответ дал:
4
Ответ:
12 см.
Объяснение:
Пусть сторона ВС= х см. Так как разность двух сторон треугольника равна 20 см, то АС= (х+20) см. Составим уравнения, используя теорему косинусов: квадрат любой стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Так как сторона треугольника не может быть отрицательным числом, то х = 12 см.
Тогда меньшая сторона треугольника равна 12 см
Приложения:
Вас заинтересует
2 года назад
3 года назад
3 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад