Question

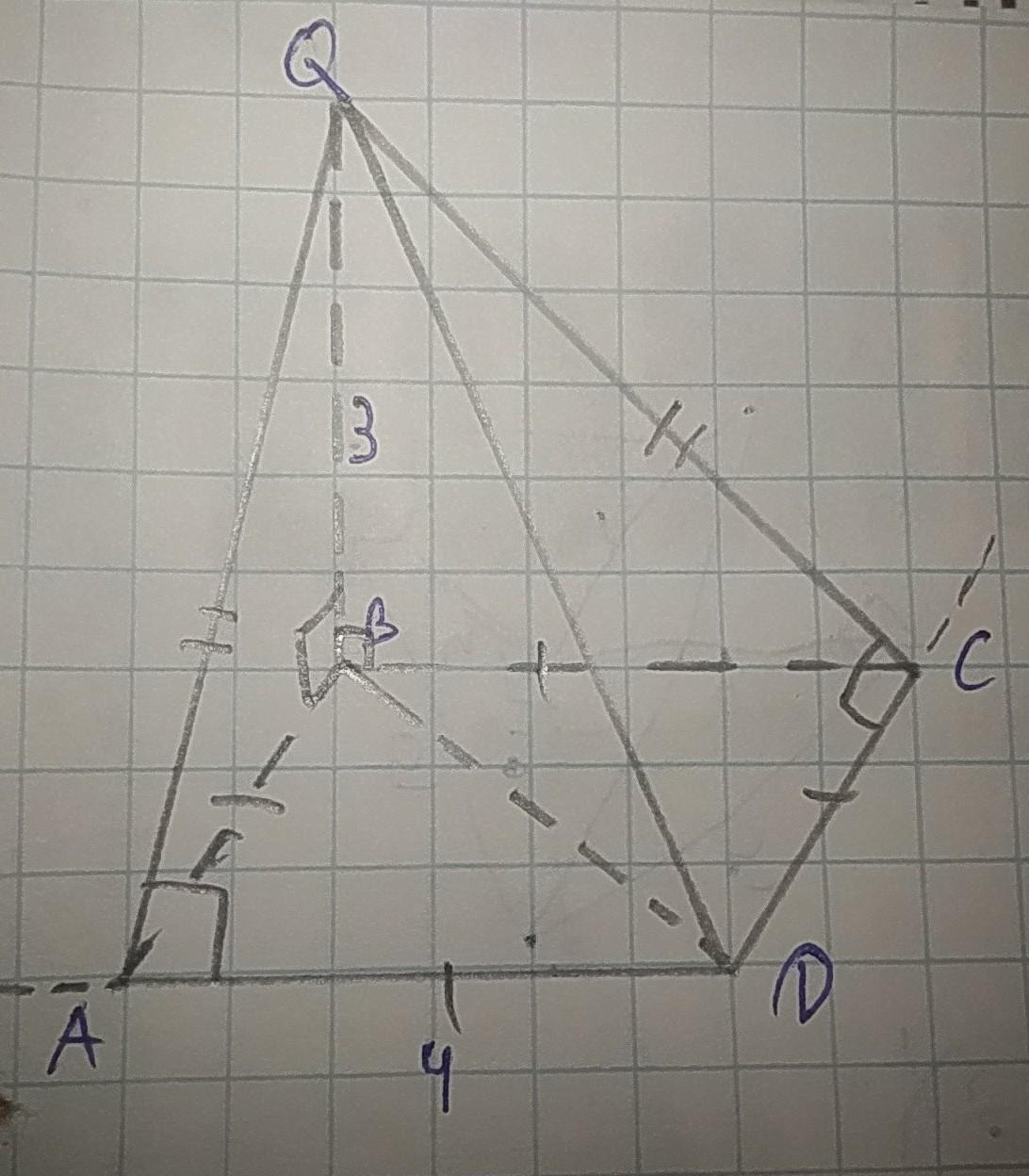
Основою піраміди є квадрат зі стороною 4 см. Одне бічне ребро перпендикулярно площині основи і дорівнює 3 см. Обчисли площу бічної поверхні.

Answer 1

Формула площі прямокутного трикутника: S = 0.5×a×b, де a і b - катети.

Трикутники QBA і QBC - рівні за першою ознакою рівності трикутників.

S = 0.5 × 3 × 4 = 6(см^2)

QA = QC = √(3^2 + 4^2) = 5(см)(т. Піфагора)

Кут QAD і QCD - прямокутні(за ТТП).

Трикутники QAD і QCD - рівні за першою ознакою рівності трикутників.

S = 0.5 × 4 × 5 = 10(см^2)

Площа бічної грані піраміди = сумі площ бічних граней = 6 + 6 + 10 + 10 = 32(см^2)