Question

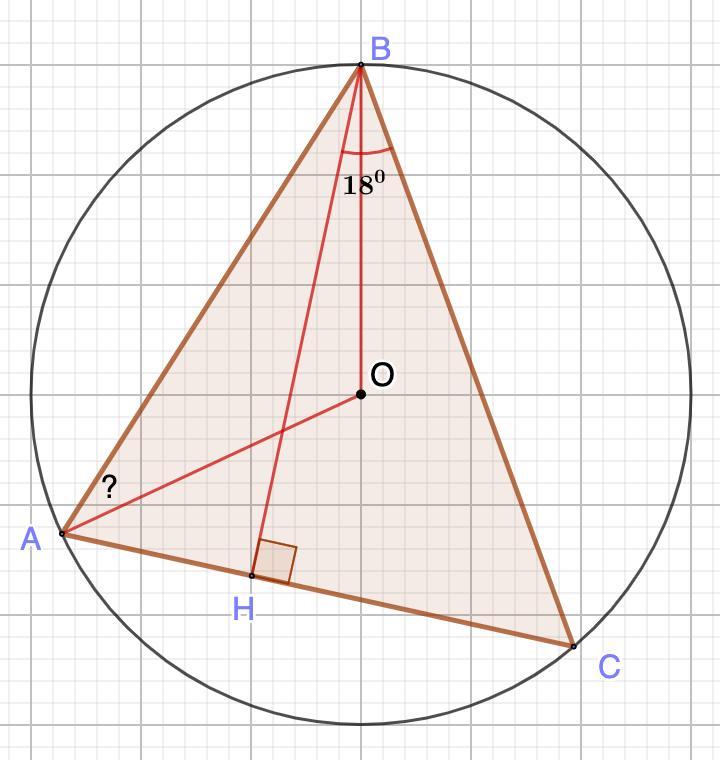
BH – высота остроугольного треугольника, O – центр окружности, описанной около этого треугольника. Найдите угол BAO, если угол HBC равен 18 градусам. срочно пожалуйста

Answer 1

Ответ:

∠ВАО = 18°

Объяснение:

Дано: ΔАВС;

Окр. О,R - описанная.

ВН - высота;

∠НВС = 18°

Найти: ∠НВС

Решение:

Рассмотрим ΔНВС - прямоугольный.

∠НВС = 18°

Сумма острых углов прямоугольного треугольника равна 90°.

⇒ ∠С = 90° - 18° = 72° - вписанный.

Вписанный угол равен половине дуги, на которую он опирается.

⇒ ∪АВ = 2∠С = 72·2=144°

Рассмотрим ΔАОВ;

АО = ОВ = R

⇒ ΔАОВ - равнобедренный.

⇒ ∠ОАВ = ∠ОВА (при основании р/б треугольника)

Центральный угол равен дуге, на которую он опирается.

⇒ ∠АОВ = ∪АВ = 144° (центральный)

Сумма углов треугольника равна 180°.

⇒ ∠ОАВ = ∠ОВА = (180°-∠АОВ):2 = (180° - 144°):2 = 18°