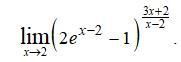Ответы
Ответ дал:
1
Здесь применен второй замечательный предел и
korshundenchik:
Спасибо)
У меня в профиле есть ещё 2 задания, ты бы не мог их посмотреть?)
Я вот сегодня сдавал это задание и у моего преподавателя возникли вопросы к этой работе и он не принял
что именно не так ?
Ну мне было бы вам проще фотографию скинуть, как это можно сделать?
Вас заинтересует
2 года назад
2 года назад
3 года назад
8 лет назад
10 лет назад