Менша основа рівнобічної трапеції дорівнюють 18 см, бічна сторона 12см, а гострий кут 60°. Знайдіть середню лінію трапеції.
Ответы
Ответ дал:
4
Ответ:
24 см.
Объяснение:
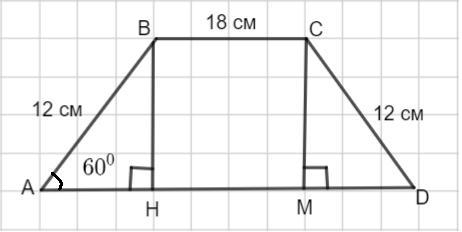
Пусть дана равнобедренная трапеция ABCD .
AB=CD=12 см , ВС= 18 см.
Проведем высоты трапеции ВН и СМ . Так как трапеция равнобедренная, то AH= MD.
Рассмотрим треугольник АНВ - прямоугольный. АВ= 12 см.
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Значит, АН= MD= 6 см.
НМ= ВС= 18 см.
Тогда AD= 6+18+6= 30 см.
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции .
Средняя линия трапеции равна полусумме оснований.
Пусть MN - средняя линия трапеции.
Значит, средняя линия трапеции равна 24 см.
Приложения:
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
8 лет назад
10 лет назад
10 лет назад