Question

Помогите пожалуйста!
Знаю, есть в интернете, но я не до конца не понимаю:(
Желательно подробно расписать и отвечать на вопросы.

Answer 1

найду ОДЗ

по свойствам логарифма x>0

делить на 0 нельзя, поэтому lnx≠0;x≠e^0;x≠1

Тогда ОДЗ x∈(0;1)∪(1;+∞)

Функция убывает , если ее производная отрицательна. поэтому найду экстремальные точки (в них производная равна 0 ) и посмотрю ее знак в полученных интервалах

Производная от частного : если y=u/v, то y`=(u`v-uv`)/v^2

u=x;u`=1; v=lnx;v`=1/x

тогда y`=(1*lnx-x*1/x)/ln^2 x=(lnx-1)/(ln x)^2   (*)

^-знак степени

y`=0; ln x-1=0; ln x=1; x=e

e≈2.7

найдена экстремальная точка х=e, осталось выяснить максимум или минимум это, Для этого проверю знаки производной на трех интервалах

а)x∈(1;e), возьму x=2 и подставлю в производную (*)

ln 2≈0.69

y`(2)=(ln2-1)/(ln2)^2= -0.31/0.69^2<0

выходит у убывает на этом интервале

б)x∈(e;+∞), возьму x=e^2=2.7^2, тогда ln(e^2)=2ln e=2*1=2

y`(e^2)=(2-1)/2^2=1/4>0, значит у на этом интервале возрастает

в)x∈(0;1), возьму x=1/e=e^(-1), ln(e^(-1))=-1

y`(1/e)=(-1-1)/(-1)^2=-2<0, значит у убывает на этом интервале

Ответ : y убывает при x∈(0;1)∪(1;e)

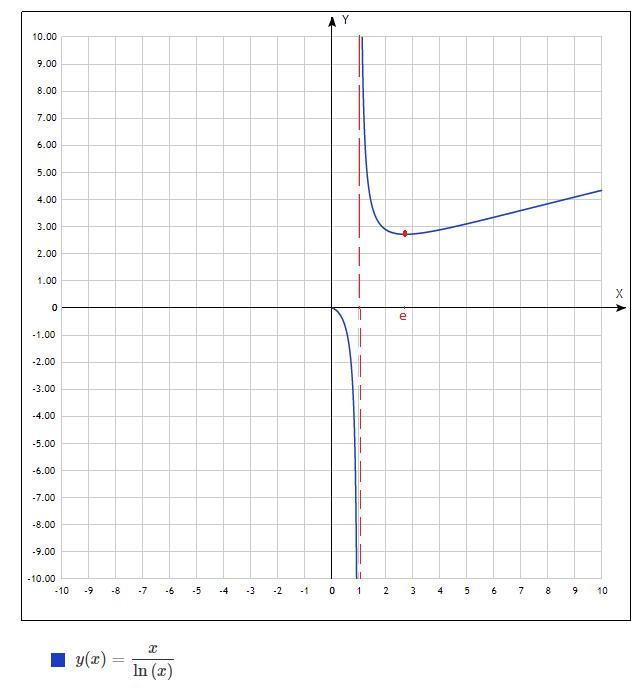
график это подтверждает, вариант ответа Б, но правая граница не входит, так как в х=е функция ни растет, ни убывает!!!