Question

Найти площадь заштрихованой

Answer 1

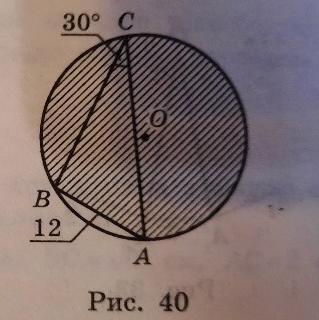
Проведем отрезки AO и BO. ∠ACB - вписанный, равен половине дуги, на которую он опирается, то есть ∪AB = 60° ⇒ ∠AOB = 60° (он центральный) ⇒ ΔAOB правильный (т.к. AO = BO - радиусы окружности). Таким образом, R = AO = BO = AB = 12.

Заштрихованная область - это S(круга) - S(сектора AOB) + S(ΔAOB). Заметим, что площадь сектора AOB = 1/6 площади круга, т.к. ∪AB = 60°.

Считаем: S = 5πR²/6 + R²√3/4 = 12(10π+3√3) - это ответ.