Question

Помогите!

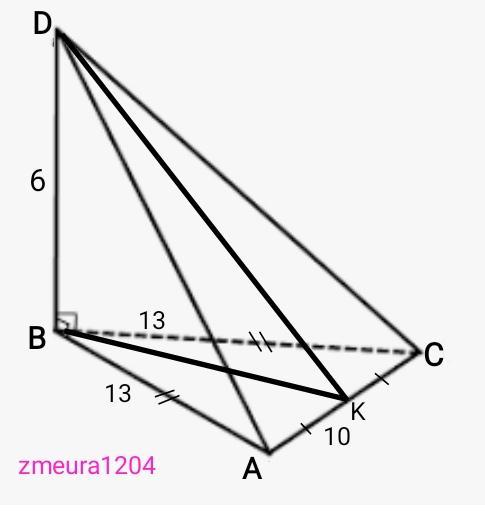
Прямая ВД перпендикулярна к плоскости треугольника АВС. Известно, что ВД=6см, АС=10 см, АВ=ВС=13 см. Найдите : а) расстояние от точки Д до прямой АС; б) площадь треугольника АСД,
С рисунком

Answer 1

Ответ:

DK=6√5см

S(∆ACD)=30√5см²

Объяснение:

BK- высота, медиана и биссектрисса равнобедренного треугольника ∆АВС.

АК=КС=АС/2=10/2=5см

По теореме Пифагора

ВК=√(АВ²-АК²)=√(13²-5²)=√(169-25)=

=√144=12см.

∆ВКС- прямоугольный треугольник

По теореме Пифагора

DK=√(DB²+BK²)=√(6²+12²)=√(36+144)=

=√180=6√5 см расстояние от точки D до прямой АС (теорема о трех перпендикулярах)

S(∆ACD)=1/2*DK*AC=1/2*6√5*10=30√5см²