Question

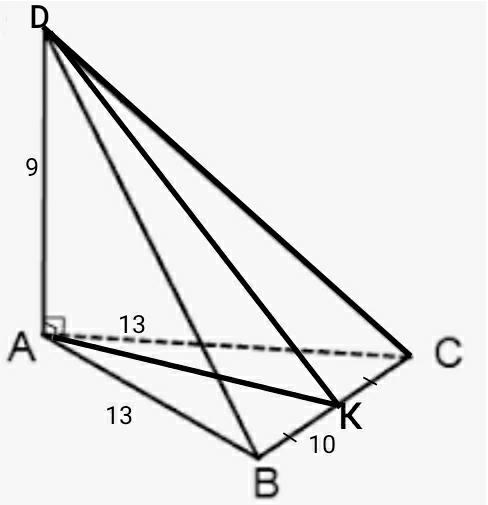
Основою піраміди DABC є трикутник АВС, у якого АВ=АС=13 см, ВС=
10 см. Ребро DA перпендикулярне до площини основи і дорівнює 9 см. Знайти
площу бічної поверхні піраміди.

Answer 1

Ответ:

192см²

Объяснение:

AK- высота, медиана и биссектрисса равнобедренного треугольника ∆АВС.

ВК=КС=5см.

∆АВК- прямоугольный треугольник

Теорема Пифагора

АК=√(АВ²-ВК²)=√(13²-5²)=12см.

∆DAK- прямоугольный треугольник

По теореме Пифагора

DK=√(DA²+AK²)=√(9²+12²)=√(81+144)=

=√225=15см.

DK⊥ВС, теорема о трех перпендикулярах.

S(∆BDC)=1/2*DK*BC=1/2*15*10=75см²

S(∆ADB)=1/2*DA*AB=1/2*9*13=58,5см²

S(∆ADB)=S(∆ADC)=58,5см²

Sбок=S(∆BDC)+2*S(∆ADB)=75+117=192см²