Question

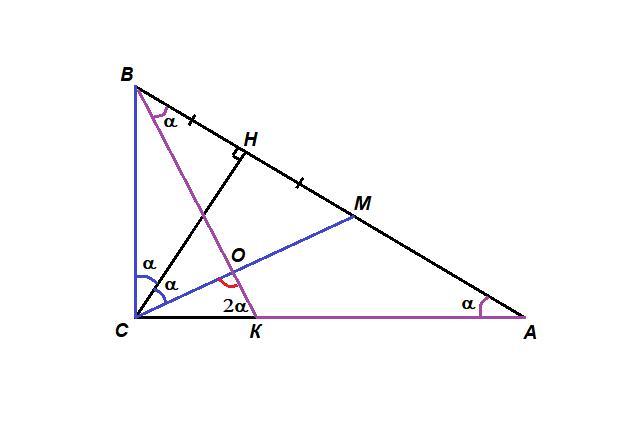
8.4 Дан прямоугольный треугольник ABC (AB – гипотенуза). На большем катете AC треугольника АВС выбрана точка К так, что АК - ВК. Пусть CH — высота треугольника ABC, и точка M сим- метрична точке В относительно точки Н. Докажите, что отрезки ВК и СМ перпендикулярны. 5 zarnych т TTTT Петрсега​

Answer 1

Ответ:

Обозначим ∠А = α.

∠СВА = 90° - α (сумма острых углов прямоугольного треугольника равна 90°)

Тогда в прямоугольном треугольнике ВСН:

∠ВСН = 90° - ∠СВА = 90° - (90° - α) = α

Точка М симметрична точке В относительно точки Н, значит

СВ = СМ,  Δ ВСМ - равнобедренный, тогда его высота СН является биссектрисой:

∠МСН = ∠ВСН = α

∠ОСК = ∠ВСА - (∠МСН + ∠ВСН) = 90° - (α + α) = 90° - 2α

_______________________

АК = ВК по условию, значит ΔАВК равнобедренный,

∠КАВ = ∠КВА = α

∠СКВ = 2α как внешний для ΔАКВ (внешний угол треугольника равен сумме двух внутренних, не смежных с ним)

Если назвать угол иначе, то ∠СКО = 2α.

В треугольнике ОСК:

∠ОСК + ∠СКО = 90° - 2α + 2α = 90°, тогда

∠СОК = 90°, следовательно

ВК⊥СМ.