Question

СРОЧНО!!!!!!!!!
Довжина відрізка середньої лінії трапеції, розташованого між її діагоналями, дорівнює 3 см. Знайдіть більшу основу трапеції, якщо її менша основа дорівнює 3 см.
СРОЧНО!!!!!!!!!!
Діагональ рівнобічної трапеції є бісектрисою її гострого кута. Знайдіть середню лінію трапеції, якщо різниця її основ дорівнює 8 см, а периметр – 36 см.​

Answer 1

Ответ:

1. 9 см; 2. 11 см

Объяснение:

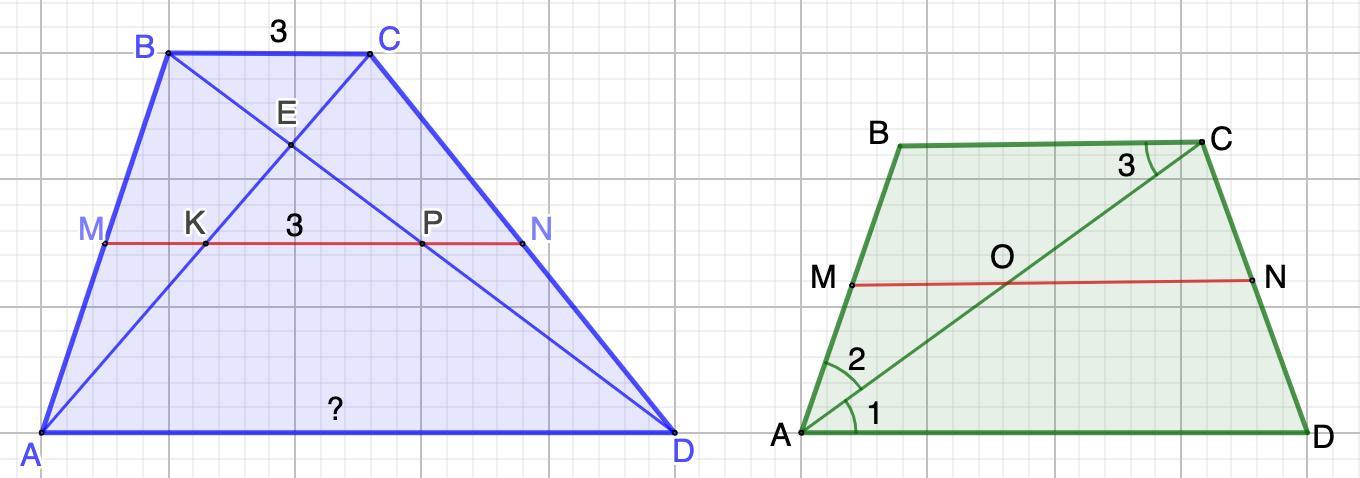
1. Дано: ABCD - трапеция.

MN - средняя линия.

КР = 3 см; ВС = 3 см.

Найти: AD

Решение:

1. Рассмотрим ΔАВС.

MN || BC; AM = MB (MN - средняя линия трапеции ABCD).

• Признак средней линии треугольника: если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей — этот отрезок можно назвать средней линией этого треугольника.

⇒ MK - средняя линия ΔАВС.

• Средняя линия треугольника равна половине основания.

⇒ MK = BC : 2 = 3 : 2 = 1,5 (см)

2. Рассмотрим ΔВСD.

MN || BC; CN = ND (MN - средняя линия трапеции ABCD).

⇒PN - средняя линия ΔВСD.

PN = BC : 2 = 3 : 2 = 1,5 (см)

3. Найдем MN:

MN = MK + KP + PN = 1,5 + 3 + 1,5 = 6 (см)

4. Рассмотрим ABCD.

MN - средняя линия.

• Средняя линия трапеции равна полусумме оснований.

⇒ MN = (BC + AD) :2

6 = (3 + AD) : 2

3 + AD = 12

AD = 9 (см)

2. Дано: ABCD - равнобедренная трапеция.

АС - диагональ, биссектриса ∠А.

AD - BC = 8 см; Р = 36 см.

Найти: MN

Решение:

1. Рассмотрим ΔАВС.

∠1 =∠2 (АС - биссектриса)

∠1 = ∠3 (накрест лежащие при BC || AD и секущей АС)

⇒ ∠2 = ∠3

• Если у треугольника два угла равны, то этот треугольник — равнобедренный.

⇒ ΔАВС - равнобедренный. ⇒ АВ = ВС

2. АВ = CD (ABCD - равнобедренная трапеция).

   АВ = ВС (п.1) ⇒ АВ = ВС = CD

Пусть АВ = ВС = CD = х см; Р=36 см

⇒ AD = 36 - 3x

По условию AD - BC = 8 см

⇒ (36 - 3х) - х = 8

4х = 28

х = 7

⇒ ВС = 7см; AD = 36 - 21 = 15(см)

⇒ MN = (BC + AD) : 2 = (7 + 15) : 2 = 11 (см)