Задача на теорию вероятностей.
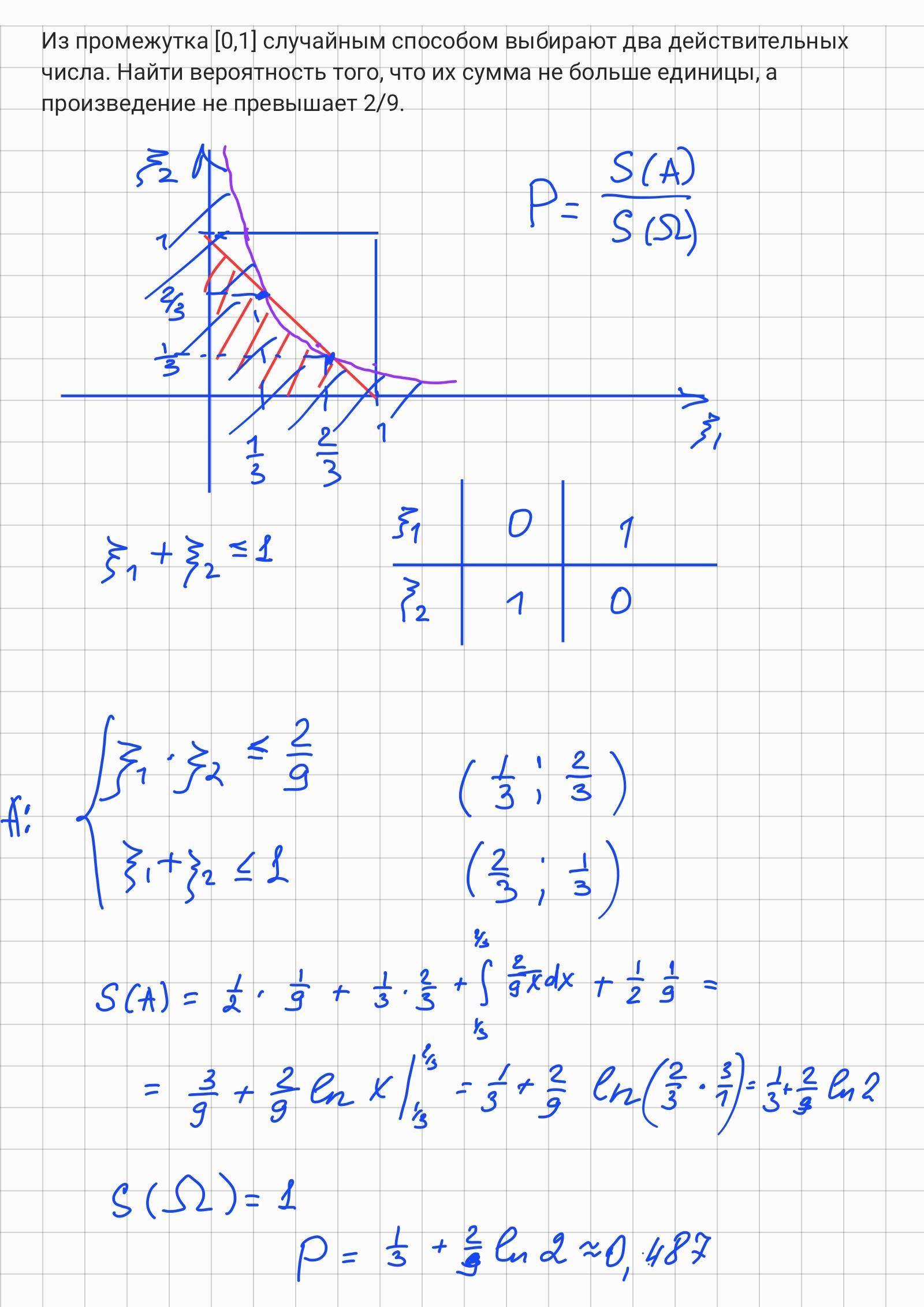
Из промежутка [0,1] случайным способом выбирают два действительных числа. Найти вероятность того, что их сумма не больше единицы, а произведение не превышает 2/9.
DNHelper:
Можно решить графическим способом через отношение площадей, по x откладываешь первое число, по y — второе число, всевозможные исходы — это квадрат площадью 1, построенный на отрезках [0, 1], [0, 1]. Нужные варианты задаются условиями x + y <= 1, xy <= 2/9. Строим графики функций y = 1 - x, y = 2/9x и находим искомую площадь как сумму интегралов от 0 до 1/3 и от 2/3 до 1 для 1 - x, от 1/3 до 2/3 для 2/9x. Получаем (7 + 4ln(2)) / 18.
1/3 и 2/3 — точки пересечения графиков.
А, сорри, обсчитался. Ответ (3 + 2ln(2)) / 9.
(3 + 2ln(2)) / 9 но это ведь площадь?
Да, это как бы "количество" нужных вариантов. Всего вариантов у нас единица.
А понял, спасибо большое
Можете ещё это решить, если не сложно? https://znanija.com/task/46503120
Ответы
Ответ дал:
1
Відповідь:
Покрокове пояснення:
Приложения:
Спасибо большое, можете ещё это решить пожалуйста, если не затруднит? https://znanija.com/task/46503120
Добрый вечер, можете пожалуйста решить данную задачу? https://znanija.com/task/46521244
Здравствуйте, Ольга, помогите пожалуйста решить задание :) https://znanija.com/task/46521707
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
8 лет назад
8 лет назад
9 лет назад