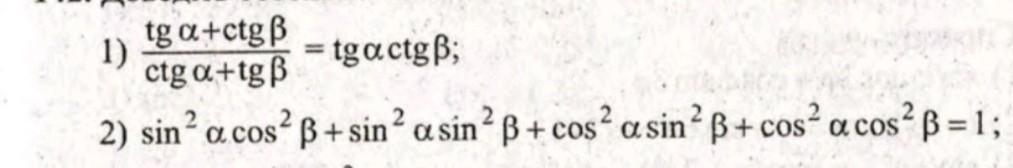Ответы
Ответ дал:
1
Ответ:
Объяснение:
1) ( tgα + ctgβ )/( ctgα + tgβ ) = tgα*ctgβ ;
( tgα + ctgβ )/( ctgα + tgβ ) = ( tgα + 1/tgβ )/( 1/tgα + tgβ ) =
= [ ( tgα*tgβ + 1 )/tgβ ] : [ ( 1 + tgα*tgβ )/tgα ] = [ ( tgα*tgβ + 1 )/tgβ ] x
x [ tgα/( tgα*tgβ + 1 ) ] = tgα * 1/tgβ = tgα*ctgβ .
Отже , дана рівність є тотожністю .
2) sin²αcos²β + sin²αsin²β +cos²αsin²β + cos²αcos²β = 1 ;
sin²αcos²β + sin²αsin²β +cos²αsin²β + cos²αcos²β = ( sin²αcos²β +
+ sin²αsin²β ) + ( cos²αsin²β + cos²αcos²β ) = sin²α( cos²β + sin²β ) +
+ cos²α( sin²β + cos²β ) = sin²α * 1 + cos²α * 1 = sin²α + cos²α = 1 .
Отже , дана рівність є тотожністю .
Вас заинтересует
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад