Question

Помогите пожалуйсто ​

Answer 1

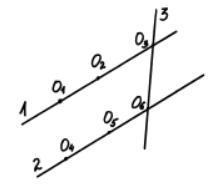
Дано: шесть точек; прямая, проходящая через любые две точки,

содержит по крайней мере еще одну из данных точек;

Доказать: все точки лежат на одной прямой;

Доказательство:

1) Данные точки можно разбить по три точки лежащие на одной

прямой;

2) Пусть точки 01,02,03 лежат на прямой 1, а точки О4, O5, О6

лежат на прямой 2;

3) Таким образом прямая проходящая через две точки, лежащие

на разных прямых, будет содержать лишь две из данных точек,

что противоречит условию задачи;

4) Следовательно все шесть данных точек лежат на одной

прямой, что и требовалось доказать.