ДОКАЖИТЕ ДВА КОРОТКИХ НЕРАВЕНСТВА ❤️❤️❤️❤️ пожалуйстааа!! С решением, ДАЮ 75 БАЛЛОВ ЗАРАНЕЕ СПАСИБО
Приложения:
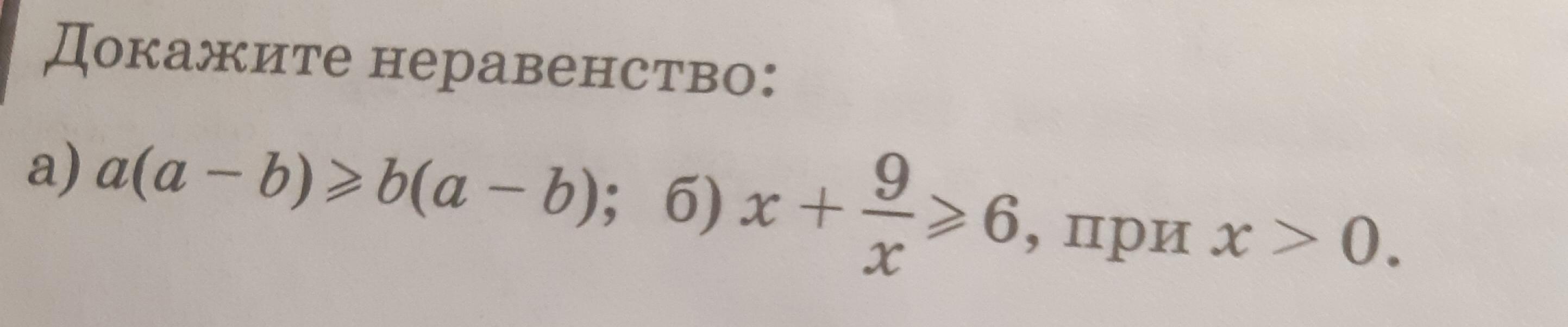
Ответы
Ответ дал:
1
Ответ:
Объяснение:
квадрат любого числа есть неотрицательное число
доказано
б)
числитель ≥ 0, знаменатель > 0 , неравенство верно, доказано
iqbj9:
спасибо!!!!
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад