Question

65 БАЛлОВ

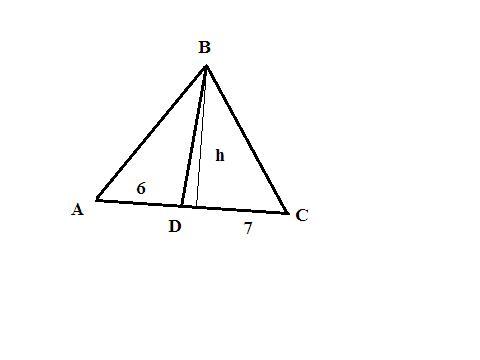
Дан треугольник ABC, на стороне AC которого взята точка D такая, что AD=6 см, а DC=7 см. Отрезок DB делит треугольник ABC на два треугольника. При этом площадь треугольника ABC составляет 117 см2.


Найди площадь меньшего из образовавшихся треугольников, ответ дай в квадратных сантиметрах

Answer 1

Ответ:

Объяснение:

Высота h треугольника АВС:

h=2S/AC где S=117, АС=AD+DC=6+7=13 см;

h=2*117/13=18 см;

высота h является общей для треугольников АВС, ABD, DBC;

площадь меньшего из треугольников -

S(ABD)=18*6/2=54 см²