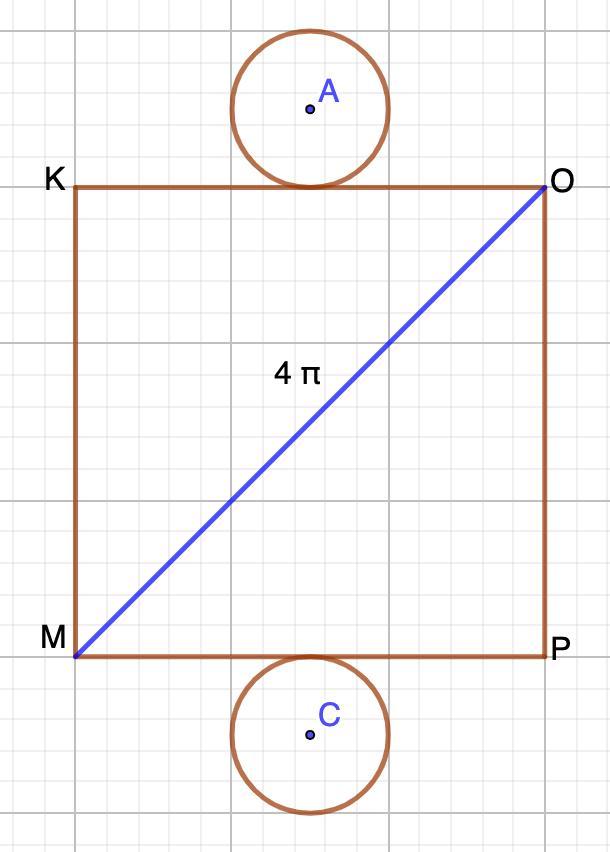
Квадрат , диагональ которого равна 4п см. является разверткой боковой поверхности цилиндра.Найдите площадь основания этого цилиндра.
Пожалуйста подробный ответ.
Пожалуйста срочно !
rimova500:
Пожалуйста срочно!
Ответы
Ответ дал:
5
Ответ:
2π
Объяснение:
Так как развертка боковой поверхности цилиндра - квадрат, то длина окружности основания будет равна стороне квадрата.
Найдем сторону квадрата. Примем сторону за а.
По теореме Пифагора:
Длина окружности равна:
Найдем радиус R:
Зная радиус, можем найти площадь:
Приложения:
Вас заинтересует
2 года назад
2 года назад
3 года назад
8 лет назад
10 лет назад