70 баллов. Объем призмы. Срочно!
Основой наклонной треугольной призмы является правильный треугольник. Если боковое ребро призмы имеет длину 8 см и наклонено к плоскости основания под углом 30°, а одна из вершин призмы проектируется в центр нижнего основания, то объем призмы равняется? Пожалуйста помогите.
Ответы
Ответ:
V = 152√3 cм³.
Объяснение:
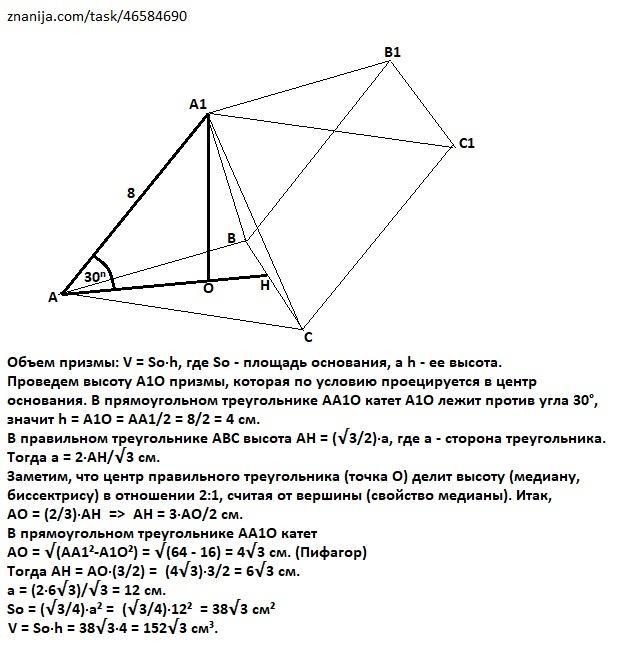
Объем призмы: V = So·h, где So - площадь основания, а h - ее высота.
Проведем высоту А1О призмы, которая по условию проецируется в центр основания. В прямоугольном треугольнике АА1О катет А1О лежит против угла 30°, значит h = A1O = AA1/2 = 8/2 = 4 см.
В правильном треугольнике АВС высота АН = (√3/2)·a, где а - сторона треугольника. Тогда а = 2·АН/√3.
Заметим, что центр правильного треугольника (точка О) делит высоту (медиану, биссектрису) в отношении 2:1, считая от вершины (свойство медианы). Итак,
АО = (2/3)·AH => AH = 3·AO/2 см.
В прямоугольном треугольнике АА1О катет
АО = √(АА1²-А1О²) = √(64 - 16) = 4√3 см. (Пифагор)
Тогда АН = АО·(3/2) = (4√3)·3/2 = 6√3 см.
а = (2·6√3)/√3 = 12 см.
So = (√3/4)·a² = (√3/4)·12² = 38√3 см²
V = So·h = 38√3·4 = 152√3 cм³.