Question

показательная функция. решить, желательно поясняя ​

Answer 1

Ответ:

$x = - 2 \: \: \: \cup \: \: \: x = 2$

Объяснение:

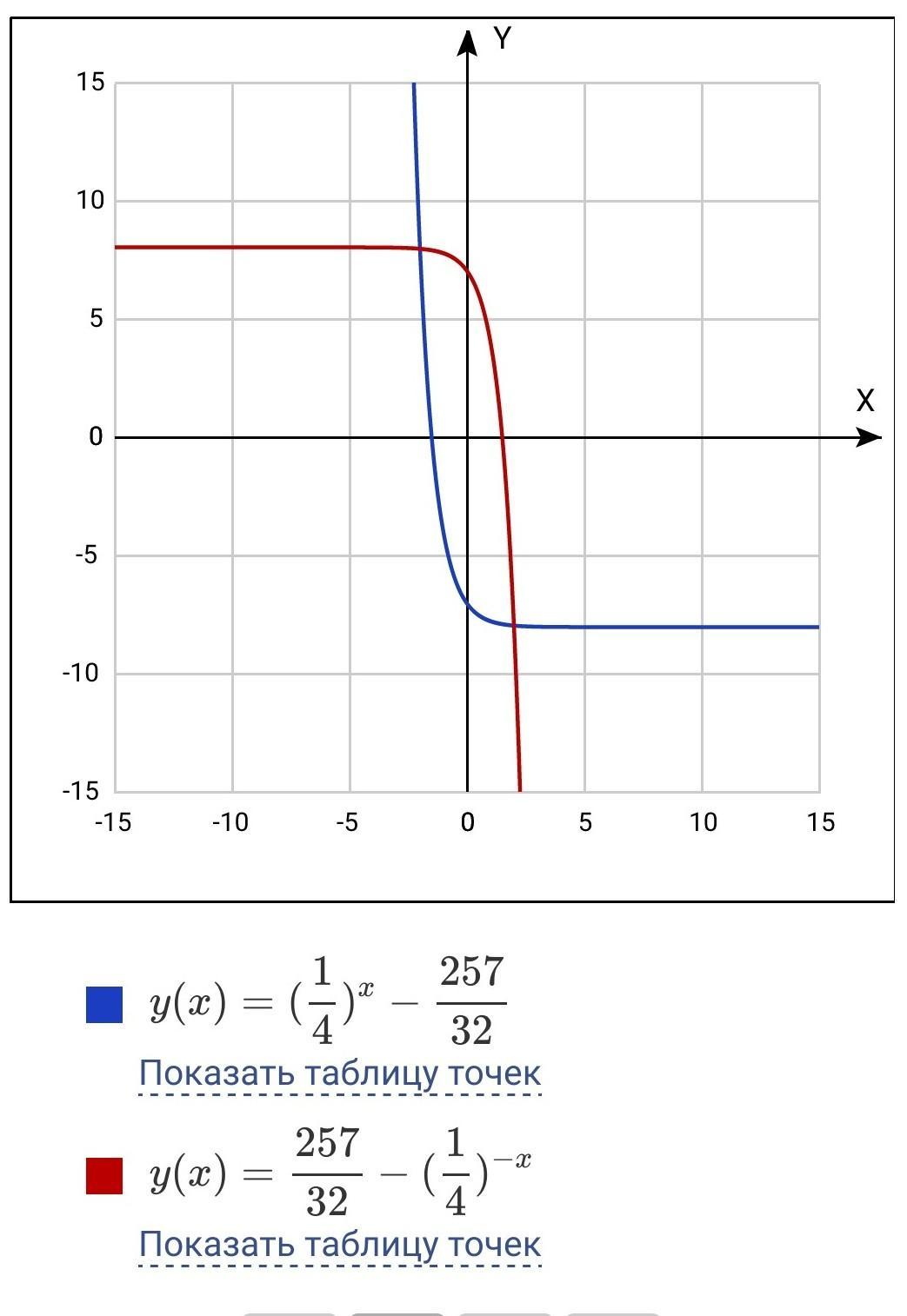
Симметрия графиков функций относительно начала координат,

т.е. относительно точки O(0;0)

говорит нам о том, что

для каждой точки которая принадлежит графику функции f(x)

существует точка симметричная ей относительно начала координат, и принадлежащая графику функции h(x)

т.е.

у точки с координатами

$A(A_x;\,A_y)$ , где $A_y=f(A_x)$

есть "сестренка" $B(B_x;\;B_y)$, где $B_y=h(B_x)$

симметричная относительно О(0;0),

и принадлежащая графику функции h(x)

Соответственно у точки B координаты $B_x$ и $B_y$ , по правилам симметрии такие, что

$B_x=-A_x$ и $B_y=-A_y$ ,

т.е. соответствующие координаты равны по модулю, но различны по знаку.

То есть, если $B_y=h(B_x);\;\, A_y=f(A_x)$, то

$B_x=-A_x \: => h(B_x)=h(-A_x);\\ \: B_y=-A_y => \: h(B_x)=-f(A_x)$

или

$B(B_x;h(B_x)) = B(-Ax;-f(A_x))\\m.k.\\Bx = -Ax;$

следовательно, если упростим и обобщим,

приняв что:

$A_x = x => B_x = -x$

$A_y = f(x) => B_y = - A_y = -f(x)$

значит:

$h(-x) = -f(x) => \: h(x) = -f(-x)$

$f(x) = \left( \frac{1}{4} \right) ^{x} - 8 \frac{1}{32} \\ \\ f(x) = - h( - x)$

$f(x) = \left( \frac{1}{4} \right) ^{x} - 8 \frac{1}{32} \\ \small{f(x) = - h( - x) \: \: < = > h( - x) = - f( x)} \\ { <}{ = > } \: h(x) = {- f}( - x) \\ \\ h(x) = - f( - x) = - \left(\left( \tfrac{1}{4} \right) ^{ - x} { -} 8 \tfrac{1}{32} \right) = \\ = 8\tfrac{1}{32} - \left( \tfrac{1}{4} \right) ^{ - x}$

$\left( \tfrac{1}{4} \right) ^{x} - 8\tfrac{1}{32}= 8\tfrac{1}{32} - \left( \tfrac{1}{4} \right) ^{ - x} \\ \left( \tfrac{1}{4} \right) ^{x} + \left( \tfrac{1}{4} \right) ^{ - x} = 8\tfrac{1}{32} +8 \tfrac{1}{32} \\ \small{m.k. \: \: { {a}^{ - x} }{ =} \tfrac{1}{ {a}^{x} } \: \: mo \: \: (\tfrac{1}{4}) }^{ - x} = { {4}^{x}} \\ \left( \tfrac{1}{4} \right) ^{x} + 4 ^{ x} = 2 \cdot \big( 8\tfrac{1}{32} \big) =16 \frac{2}{32} {= }16 \frac{1}{16}$

После замены

${4}^{x} = t \: = > \: \: ( \frac{1}{4} )^{x} = \frac{1}{t} \\ t + \frac{1}{t} = 16 \frac{1}{16}$

Очевидно, что уравнение приводится к квадратному с корнями

$t_{1} = 16; \: t_{2} = \frac{1}{16}$

Обратная замена:

$( \tfrac{1}{4})^{x} = 16 ; \: \: \cup \: \: \: ( \tfrac{1}{4})^{x} = \tfrac{1}{16 } ; \: \\ {4}^{ - x} = 16 \: \: \cup \: \: \frac{1}{ {4}^{x} } = \frac{1}{16} \\ {4}^{ - x} = {4}^{2} \: \: \cup \: \: \frac{1}{ {4}^{x} } = \frac{1}{ {4}^{2} } \\ x = - 2 \: \: \: \cup \: \: \: x = 2$

Собственно, это и есть ответ.