Question

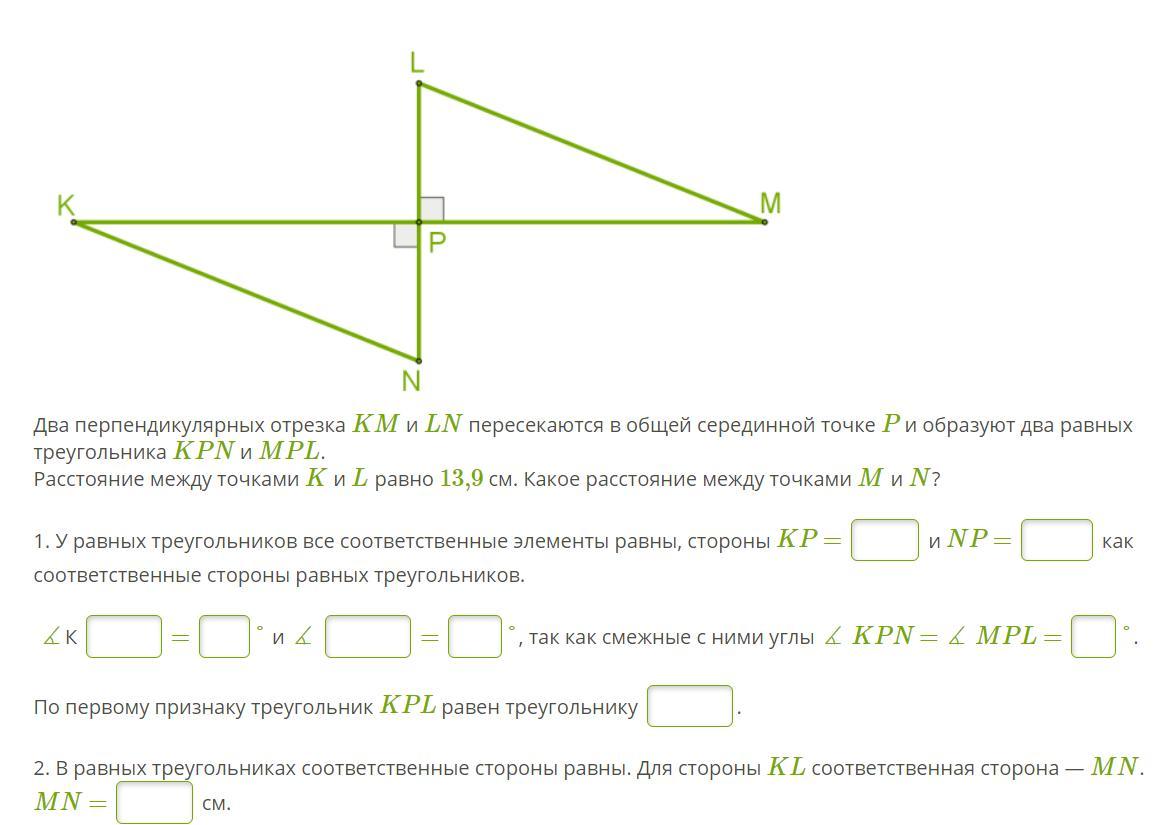
Два перпендикулярных отрезка KM и LN пересекаются в общей серединной точке P и образуют два равных треугольника KPN и MPL.
Расстояние между точками K и L равно 13,9 см. Какое расстояние между точками M и N?

1. У равных треугольников все соответственные элементы равны, стороны KP =
и NP =
как соответственные стороны равных треугольников.

∡К
=
° и ∡
=
°, так как смежные с ними углы ∡ KPN = ∡ MPL =
°.

По первому признаку треугольник KPL равен треугольнику
.

2. В равных треугольниках соответственные стороны равны. Для стороны KL соответственная сторона — MN.
MN =
см.

Answer 1

Ответ:

1.У равных треугольников все соответствующие элементы равны, стороны KP=MP и NP=LP как соответственные стороны равных треугольников.

∡ KPL= 90° и ∡ MPN=90° так как смежные с ними углы ∡ KPN= ∡ MPL=90°

По первому признаку треугольник KPL равен треугольнику MPN.

2.В равных треугольниках соответственные стороны равны. Для стороны KL соответственная сторона-MN. MN=13.9 см

Объяснение:

полностью написал твое решение)