Question

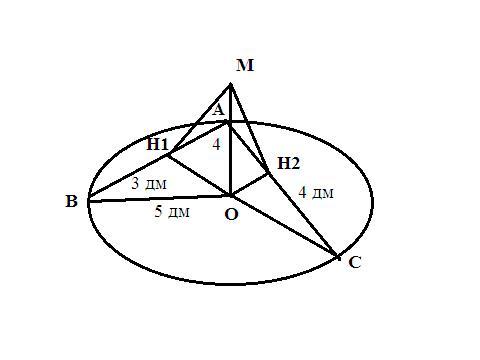
Из точки А окружности, радиус которой равен 5 дм, проведены две хорды АВ=6 дм и АС=8 дм. Из центра О окружности к ее плоскости восстановлен перпендикуляр ОМ, длина которого равна 4 дм. Найдите расстояние от точки М до каждой из этих хорд.
Геометрия 10 класс самбади хелп.

Answer 1

Ответ:

Объяснение:

Расстояние от М до хорд АВ и АС - перпендикуляр, проведенный от М к этим хордам. От центра О окружности проводим перпендикуляр к хордам АВ и АС. Он делит хорды пополам.

ΔВН₁О прямоугольный ОВ=5 дм (радиус) ВН₁=АВ/2=3 дм, тогда по т. Пифагора ОН₁=√(5²-3²)=4 дм;

ΔОН₁М прямоугольный, ОМ=4 дм ОН₁=4 дм, по т. Пифагора:

Н₁М=√(4²+4²)=4√2 дм - расстояние от М до хорды АВ;

аналогично:

ΔВН₂О прямоугольный ОВ=5 дм (радиус) СН₂=АС/2=4 дм, тогда по т. Пифагора ОН₁=√(5²-4²)=3 дм;

ΔОН₂М прямоугольный, ОМ=4 дм ОН₂=3 дм, по т. Пифагора:

Н₂М=√(4²+3²)=5 дм - расстояние от М до хорды АС.