Доброго времени суток господа, мне нужна помощь с логарифмическим неравенством.
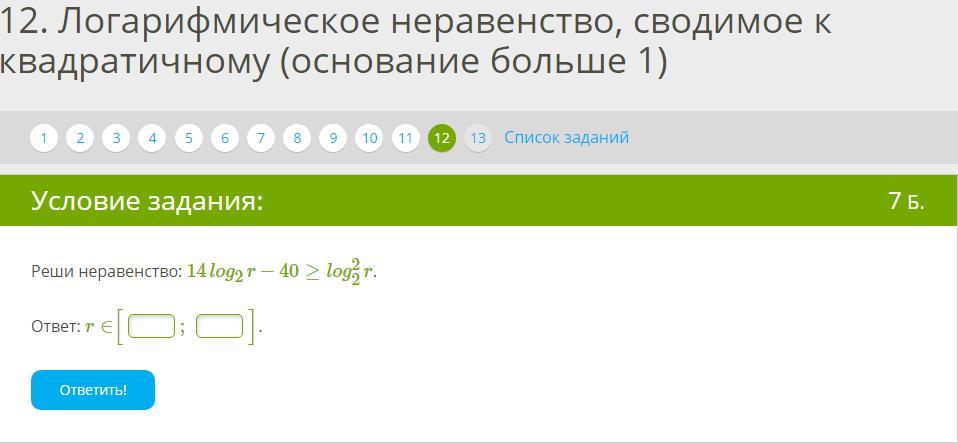
14log2(r)−40≥(log2(r))^2
Приложения:
Ответы
Ответ дал:
1
Ответ:
r €[16;1024]
Пошаговое объяснение:
ОДЗ:
r>0
логарифмическое квадратное неравенство, замена переменной:
метод интервалов:
1).
3).
+++++[4] ------ [10] ++++++> t
4).
обратная замена:
простейшее логарифмическое неравенство, основание логарифма а=2, 2>1, => знак неравенства не меняем
учитывая ОДЗ, получим
r€[16; 1024]
,знак € читать "принадлежит"
Вас заинтересует
2 года назад
3 года назад
3 года назад
8 лет назад
10 лет назад