Question

НУЖНО ВЫЧИСЛИТЬ ПРЕДЕЛ, С РЕШЕНИЕМ НОРМАЛЬНЫМ, ПЖЖЖЖ!!!!

Answer 1

Ответ:

Объяснение:

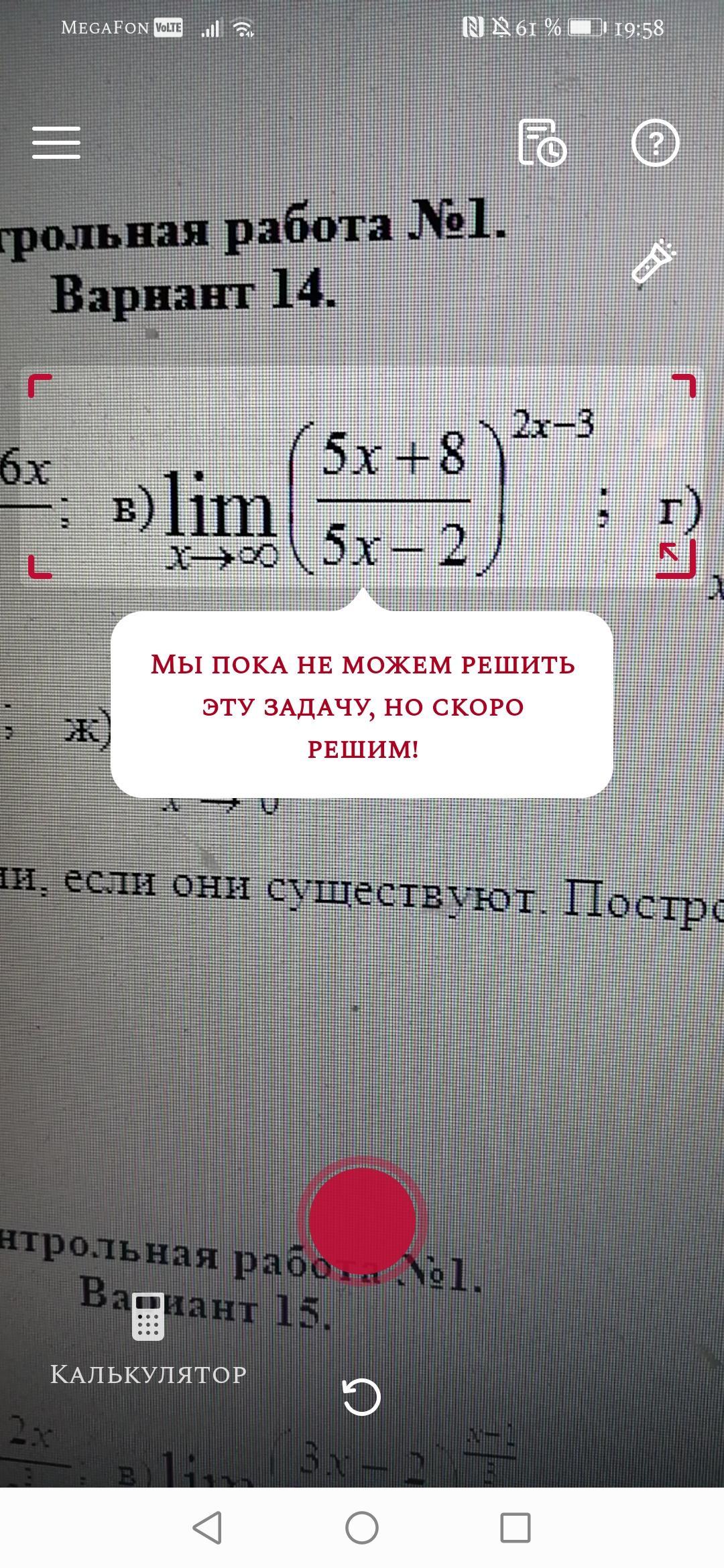
приведем предел (5x+8)/(5x-2) ко второму замечательному пределу

lim ( (1+(1/n))^n))=e это второй замечательный предел

n->∞  

с помощью замены переменных

(5x+8)/(5x-2)=(5x-2+10)/(5x-2)=1+(10/(5x-2))

обозначим

(10/(5x-2))=1/y

10y=5x-2  

x=(10y+2)/5

2x-3=2(10y+2)/5 - 3= ((20y+4)/5)-3=4y+(4/5)-3=4y-(19/5)

сделаем замену переменных

(5x+8)/(5x-2))^(2x-3)=(1+(1/y))^(4y-(19/5))=((1+(1/y))^y)⁴(1+(1/y))^(-19/5)

10y=5x-2

y=(5x-2)/10

при х->∞  ⇒ y->∞

lim  (5x+8)/(5x-2))^(2x-3)=

x->∞

=lim ((1+(1/y))^y)⁴(1+(1/y))^(-19/5)=

y->∞

=(lim ((1+(1/y))^y)) ⁴ * (lim (1+(1/y))) ^(-19/5)=

  y->∞                      y->∞

' lim ((1+(1/y))^y))=e это второй замечательный предел

' x->∞  

' (1/y)->0

' (lim (1+(1/y)))=1

' y->∞

=e⁴*1^(-19/5) =e⁴*1=e⁴