Ответы
Ответ дал:
14
Ответ:
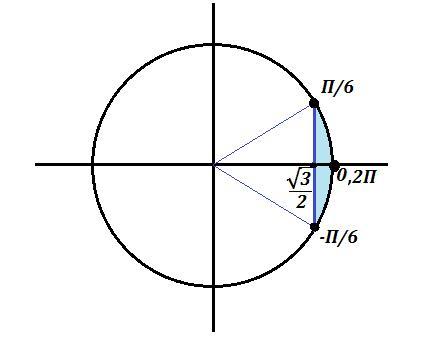
Целых решений на (0;2П) нет .
Приложения:
Аноним:
снесщ
капец как круто
правильно
Вас заинтересует
2 года назад
2 года назад
3 года назад
8 лет назад
9 лет назад